Next: Wasserstoffhäufigkeit Up: Elektronendichte Previous: Methode nach Inglis und
![]()
![]()
![]()
Next: Wasserstoffhäufigkeit
Up: Elektronendichte
Previous: Methode nach Inglis und
In Sternatmosphären wird der Stark-Effekt nicht durch ein gleichförmiges, konstantes elektrisches Feld erzeugt. Zur realistischen Beschreibung des Effekts muß man vielmehr den gleichzeitigen Einfluß einer größeren Anzahl sich bewegender, felderzeugender Teilchen berücksichtigen. J. Holtsmark berechnete die Wahrscheinlichkeitsverteilung der am Ort des strahlenden Atoms herrschenden Feldstärke und zeigte, daß man bei dieser Betrachtungsweise für den Absorptionskoeffizienten der resultierenden Linie
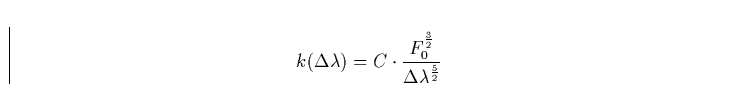 |
(8) |
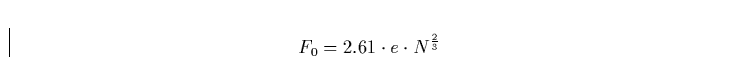 |
(9) |
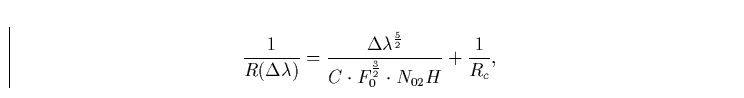 |
(10) |
Hierzu trage man für beide Flügel von H![]()
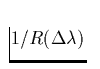 gegen
gegen 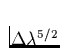 auf (mit
auf (mit 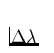 [Å] Abstand von
Linienzentrum) und berechne N aus der Steigung (Mittelwert) der
resultierenden Geraden. Zur Interpretation von N gilt die gleiche
Argumentation wie unter 3.1.
[Å] Abstand von
Linienzentrum) und berechne N aus der Steigung (Mittelwert) der
resultierenden Geraden. Zur Interpretation von N gilt die gleiche
Argumentation wie unter 3.1.
Sterne frühen Spektraltyps können eine beträchtliche
Rotationsgeschwindigkeit 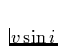 aufweisen. Wie können die mit den
beiden Methoden ermittelten Werte für Ne in diesem Zusammenhang
interpretiert werden? Welcher Wert sollte für die weitere Berechnung
benutzt werden?
aufweisen. Wie können die mit den
beiden Methoden ermittelten Werte für Ne in diesem Zusammenhang
interpretiert werden? Welcher Wert sollte für die weitere Berechnung
benutzt werden?
Roberto Saglia