Next: AUFGABEN Up: No Title Previous: Methode nach Holtsmark (R2)
![]()
![]()
![]()
Next: AUFGABEN
Up: No Title
Previous: Methode nach Holtsmark (R2)
Mit der Elektronendichte Ne, der Säulendichte N02H und der Atmosphärentemperatur T kann man nun vollends die Wasserstoffhäufigkeit mittels der Boltzmann- und Sahaformel bestimmen. Welche Voraussetzung muß aber bei einem solchen Vorgehen erfüllt sein?
Die Boltzmannformel beschreibt die thermische Anregung von Atomen bzw. Ionen und lautet in der für die astrophysikalische Anwendung auf Wasserstoff nützlichen Form:
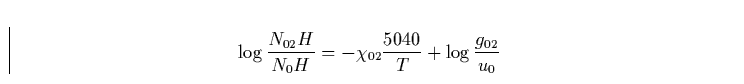 |
(11) |
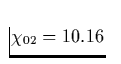 eV die Anregungsenergie des 2.
Quantenzustandes, g02 = 2n2 = 8 das statistische Gewicht dieses
Zustandes und
eV die Anregungsenergie des 2.
Quantenzustandes, g02 = 2n2 = 8 das statistische Gewicht dieses
Zustandes und 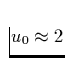 (warum gilt hier diese Näherung?) die
Zustandssumme des neutralen Wasserstoffs. Damit ergibt sich N0H, die
Säulendichte der neutralen Wasserstoffatome.
(warum gilt hier diese Näherung?) die
Zustandssumme des neutralen Wasserstoffs. Damit ergibt sich N0H, die
Säulendichte der neutralen Wasserstoffatome.
Die Sahaformel beschreibt die Besetzung zweier aufeinenderfolgender Ionisationszustände und lautet entsprechend:
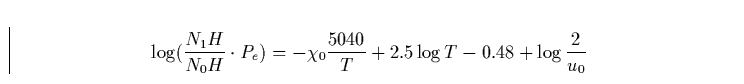 |
(12) |
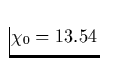 eV die Ionisationsenergie von Wasserstoff,
eV die Ionisationsenergie von Wasserstoff,
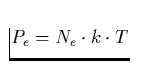 [dyn cm-2] der Elektronendruck und
[dyn cm-2] der Elektronendruck und 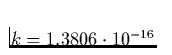 erg K-1 die Boltzmannkonstante. Damit ergibt sich N1H,
die Säulendichte der ionisierten Wasserstoffatome.
erg K-1 die Boltzmannkonstante. Damit ergibt sich N1H,
die Säulendichte der ionisierten Wasserstoffatome.
Mit N0H + N1H =NH folgt die Säulendichte des gesamten Wasserstoffs. Wieviel Prozent hiervon sind ionisiert?
Nach allgemeinem astrophysikalischem Brauch gebe man bei allen Häufigkeitsangaben den Logarithmus des entsprechenden Wertes an!