Next: Methode nach Holtsmark (R2) Up: Elektronendichte Previous: Elektronendichte
![]()
![]()
![]()
Next: Methode nach Holtsmark (R2)
Up: Elektronendichte
Previous: Elektronendichte
Die Aufspaltung der Terme (2n - 1) und damit die Verbreiterung der Linien
(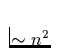 ) wächst mit der Hauptquantenzahl n bei gegebener Dichte der
felderzeugenden Teilchen N [cm-3] rasch an. Von einem bestimmten
n=nm an werden sich die Flügel benachbarter Linien so überlagert
haben, daß die Serie (in unserem Fall die Balmerserie) schon vor Erreichen
der theoretischen Grenze (
) wächst mit der Hauptquantenzahl n bei gegebener Dichte der
felderzeugenden Teilchen N [cm-3] rasch an. Von einem bestimmten
n=nm an werden sich die Flügel benachbarter Linien so überlagert
haben, daß die Serie (in unserem Fall die Balmerserie) schon vor Erreichen
der theoretischen Grenze (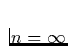 ) abbricht und keine Linie mehr zu
sehen ist. Diese vollständige Überlappung der Linien tritt umso früher
ein, je stärker das Feld, d.h. je größer N ist. D.R. Inglis und
E.Teller haben gezeiget, daß zwischen der Hauptquantenzahl nm der
letzten, gerade noch getrennt beobachtbaren Linie und N folgender
einfacher Zusammenhang besteht:
) abbricht und keine Linie mehr zu
sehen ist. Diese vollständige Überlappung der Linien tritt umso früher
ein, je stärker das Feld, d.h. je größer N ist. D.R. Inglis und
E.Teller haben gezeiget, daß zwischen der Hauptquantenzahl nm der
letzten, gerade noch getrennt beobachtbaren Linie und N folgender
einfacher Zusammenhang besteht:
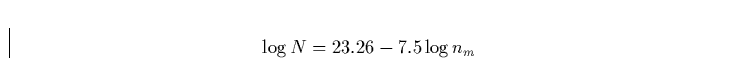 |
(6) |
N repräsentiert hier zunächst Ionen und Elektronen. Aber nur, wenn für die Atmosphärentemperatur T des Sterns die Beziehung
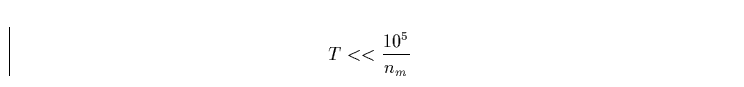 |
(7) |
Roberto Saglia