Next: Elektronendichte Up: No Title Previous: Linienprofil
![]()
![]()
![]()
Next: Elektronendichte
Up: No Title
Previous: Linienprofil
Die abrupte Änderung des kontinuierlichen Intensitätsverlaufes an der Grenze der Balmerserie kann zur Bestimmung der Häufigkeit von Wasserstoffatomen im 2. Quantenzustand benützt werden. Dieser sogenannte Balmersprung ist definiert durch
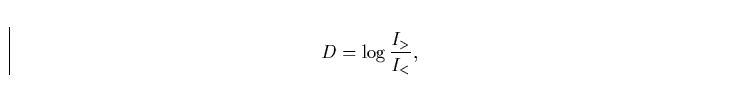 |
(4) |
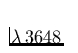 Å ist. In der
Praxis beobachtet man oft keinen sehr ausgeprägten Sprung, da der
Kontinuumsverlauf auf der langwelligen Seite durch die Überlagerung der
dicht aufeinenderfolgenden Balmerlinien mehr oder weniger stark
verfälscht ist. Zur Bestimmung von D messe man daher bei mehreren
geeigneten Wellenlängen die Intensität (I;SPMgt;, I;SPMlt;) des
ungestörten Kontinuums, trage
Å ist. In der
Praxis beobachtet man oft keinen sehr ausgeprägten Sprung, da der
Kontinuumsverlauf auf der langwelligen Seite durch die Überlagerung der
dicht aufeinenderfolgenden Balmerlinien mehr oder weniger stark
verfälscht ist. Zur Bestimmung von D messe man daher bei mehreren
geeigneten Wellenlängen die Intensität (I;SPMgt;, I;SPMlt;) des
ungestörten Kontinuums, trage 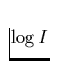 gegen
gegen 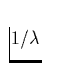 auf und
extrapoliere linear von beiden Seiten der Sprungstelle bis zur
Wellenlänge 3648Å.
auf und
extrapoliere linear von beiden Seiten der Sprungstelle bis zur
Wellenlänge 3648Å.
Dem Balmersprung D entspricht bezogen auf das Kontinuum der langwelligen Seite eine Einsenkung
| RD = 1 - 10-D , | (5) |
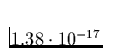 cm2. Damit ergibt sich mit (2) die
Säulendichte der absorbierenden H-Atome N02H, d.h. die Anzahl der
H-Atome N02 in einer Säule der Höhe H mit einem Querschnitt von
1cm2.
cm2. Damit ergibt sich mit (2) die
Säulendichte der absorbierenden H-Atome N02H, d.h. die Anzahl der
H-Atome N02 in einer Säule der Höhe H mit einem Querschnitt von
1cm2.
Roberto Saglia