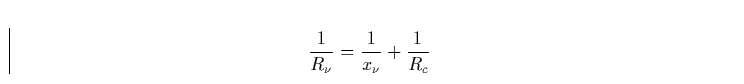Next: Balmersprung (R1)
Up: No Title
Previous: Datenreduktion
Das Profil einer Spektrallinie wird durch die relativen Linieneinsenkungen
| 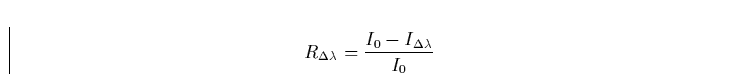 |
(1) |
beschrieben, wobei I0 die Intensität des wahren Kontinuums und
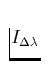 die in der Linie im Abstand
die in der Linie im Abstand 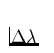 von der
Linienmitte gemessene Intensität bedeuten.
von der
Linienmitte gemessene Intensität bedeuten.
Entstehen Linien in optisch dünner Schicht (homogene Atmosphäre, reine
Absorption), dann gilt für die Linieneinsenkung bei einer bestimmten
Frequenz 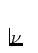
|  |
(2) |
wobei 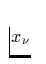 die optische Dicke,
die optische Dicke, 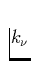 der Absorptionskoeffizient pro
Teilchen, N die Zahl der absorbierenden Teilchen pro cm3 und H die
effektive Atmosphärenhöhe (in cm) ist. Diese Beziehung ist nur für
schwache Linien und für die Flügel starker Linien gültig. Für
größere optische Dicken existiert kein einfacher Zusammenhang mehr
zwischen
der Absorptionskoeffizient pro
Teilchen, N die Zahl der absorbierenden Teilchen pro cm3 und H die
effektive Atmosphärenhöhe (in cm) ist. Diese Beziehung ist nur für
schwache Linien und für die Flügel starker Linien gültig. Für
größere optische Dicken existiert kein einfacher Zusammenhang mehr
zwischen 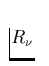 und
und 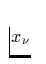 , lediglich die relative Einsenkung in der
Linienmitte der resultierenden starken Absorptionslinie strebt einem
Grenzwert Rc zu. Diese Grenzfälle starker und schwacher Absorption kann
man bei nicht allzu großen Ansprüchen an die Genauigkeit mit der
Interpolationsformel
, lediglich die relative Einsenkung in der
Linienmitte der resultierenden starken Absorptionslinie strebt einem
Grenzwert Rc zu. Diese Grenzfälle starker und schwacher Absorption kann
man bei nicht allzu großen Ansprüchen an die Genauigkeit mit der
Interpolationsformel
| 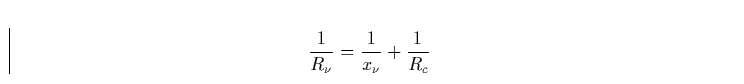 |
(3) |
verbinden und damit das Profil einer beliebigen Linie angenähert beschreiben.
Dabei ist Rc nicht die Grenzeinsenkung der untersuchten Linie, sondern
der Mittelwert aus den stärksten Linien im Spektrum.



Next: Balmersprung (R1)
Up: No Title
Previous: Datenreduktion
Roberto Saglia
5/13/1998
![]()
![]()
![]()
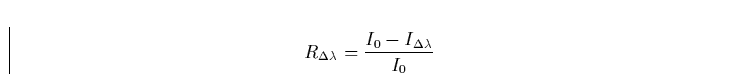
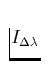 die in der Linie im Abstand
die in der Linie im Abstand 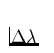 von der
Linienmitte gemessene Intensität bedeuten.
von der
Linienmitte gemessene Intensität bedeuten.
![]()