 in Table 1.
in Table 1.
After having typed @@ dodel, you will be asked to give a name of a frame, which will then appear on the screen. Try to identify possible morphological properties of the galaxy. Can you see a disk? Can you see spiral arms? Is there a bar?
Following the instructions, measure first the value of the sky (in
counts per pixel) with the cursor in several positions around the
galaxy and type the average in. Is the sky background flat? For one
frame, quantify the percentage variations of its value across the
image and compare this value with the expected shot noise (see
Eq. 2 with 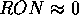 ). Then measure the position of
the center of the galaxy, and finally, delete all of the (foreground)
stars or unwanted objects around the galaxy with cursor. The frame
will appear on the screen with black spots where deletions were
made. Check that all of the unwanted objects have been deleted. If
some are still present, delete them with the command @@
domoredel. Now you are ready to run @@ docog. The scale of the
telescope+CCD detector system
). Then measure the position of
the center of the galaxy, and finally, delete all of the (foreground)
stars or unwanted objects around the galaxy with cursor. The frame
will appear on the screen with black spots where deletions were
made. Check that all of the unwanted objects have been deleted. If
some are still present, delete them with the command @@
domoredel. Now you are ready to run @@ docog. The scale of the
telescope+CCD detector system![]() is 0.396 arcsec/pixel. Now you
have created a file with extension .cog (for example, 691016222.cog).
is 0.396 arcsec/pixel. Now you
have created a file with extension .cog (for example, 691016222.cog).
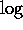 of the distance from the center with the
command plquat file or plexp file, where file is,
for example, 691016222. You can obtain hardcopies of the plots by
typing device postland, executing the plotting programs
once more and giving again device x11.
of the distance from the center with the
command plquat file or plexp file, where file is,
for example, 691016222. You can obtain hardcopies of the plots by
typing device postland, executing the plotting programs
once more and giving again device x11.
Classify the galaxy as elliptical, spiral or S0 with the help of these
plots, of the morphological information you collected in the previous
step, and by comparing the central surface brightnesses. Use the
brightness of the sky in the R band (20.63 mag/arcsec ) to get the
calibration (see Eq. 13). Determine its flattening (if it is an
elliptical) or its inclination angle, from the ellipticity you measured above.
Get a first estimate of
) to get the
calibration (see Eq. 13). Determine its flattening (if it is an
elliptical) or its inclination angle, from the ellipticity you measured above.
Get a first estimate of 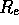 or
h drawing a line on these plots (see Eq. 14 and
15).
or
h drawing a line on these plots (see Eq. 14 and
15).
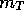 , the
half-luminosity radii
, the
half-luminosity radii 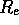 and the average surface brightnesses
and the average surface brightnesses
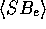 of the galaxies, knowing the sky in the R band (see
Eq. 13 and point (4) above). Use both methods described in
Section 2.4.
of the galaxies, knowing the sky in the R band (see
Eq. 13 and point (4) above). Use both methods described in
Section 2.4.
Compare the values of 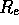 determined here with those obtained
above. For one galaxy determine what would be the change in
determined here with those obtained
above. For one galaxy determine what would be the change in 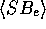 if your determination of the sky would have been wrong by
if your determination of the sky would have been wrong by 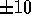 % (you
do not need to derive again the curve of growth).
% (you
do not need to derive again the curve of growth).
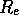 into Kpc. If D is the distance of the object
in Mpc (240 for A2593, see Sect. 1), one has:
into Kpc. If D is the distance of the object
in Mpc (240 for A2593, see Sect. 1), one has:
where the numerical factor converts arcsec into radiants. Convert
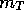 into absolute values
into absolute values 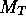 using Eq. 6. Convert
using Eq. 6. Convert 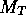 into solar luminosities, remembering that the R band solar luminosity
is
into solar luminosities, remembering that the R band solar luminosity
is 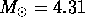 . You do not need to convert
. You do not need to convert 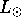 into erg/s:
Eq. 8 gives the ``number of suns'' present in the galaxy.
into erg/s:
Eq. 8 gives the ``number of suns'' present in the galaxy.
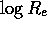 against
against 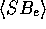 and
and 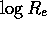 against
against 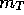 . Draw the ``best-fit'' lines to these points and determine
the coeffecients a and b of Eq. 22 and c and d
for Eq. 23. Estimate
the standard deviation (rms) around these relations. How this translate
on the precision of the estimate of the distance of the cluster (see Eq.
24)? How can Eq. 23 be used to estimate distance ratios?
. Draw the ``best-fit'' lines to these points and determine
the coeffecients a and b of Eq. 22 and c and d
for Eq. 23. Estimate
the standard deviation (rms) around these relations. How this translate
on the precision of the estimate of the distance of the cluster (see Eq.
24)? How can Eq. 23 be used to estimate distance ratios?
 in Table 1, repeating what described above.
The sky in the B band is 22.17 mag/arcsec
in Table 1, repeating what described above.
The sky in the B band is 22.17 mag/arcsec .
Compute the total magnitude in the B band
.
Compute the total magnitude in the B band 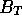 using the fact that the
total magnitude of the sun in the B band is 5.48. Finally, compute the
total colour
using the fact that the
total magnitude of the sun in the B band is 5.48. Finally, compute the
total colour 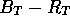 . Discuss the results having in mind the classification
of these objects.
. Discuss the results having in mind the classification
of these objects.
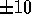 %. To do this, open a MIDAS session and give
the MIDAS command write/descr file himmel/r/1/1 value. Running
again @@ docog). Quit the MIDAS session and enter in
SUPERMONGO. Plot the resulting profile with plquat file.
Discuss the results in view of galaxy classification.
%. To do this, open a MIDAS session and give
the MIDAS command write/descr file himmel/r/1/1 value. Running
again @@ docog). Quit the MIDAS session and enter in
SUPERMONGO. Plot the resulting profile with plquat file.
Discuss the results in view of galaxy classification.

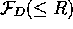 using Eq. 15 and 16.
using Eq. 15 and 16.
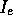 and
and 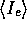 .
.
 .
.
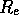 in arcsec and Kpc,
in arcsec and Kpc, 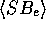 ,
, 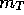 ,
,
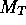 ,
, 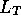 for the 9 galaxies analyzed, as determined from
the analysis of the R frames. Quote the percentage
error on
for the 9 galaxies analyzed, as determined from
the analysis of the R frames. Quote the percentage
error on 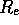 that you get by comparing the different methods of
points (4) and (5). Quote the variations of
that you get by comparing the different methods of
points (4) and (5). Quote the variations of 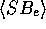 expected from point (5).
expected from point (5).
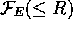 using Eq. 14 and 16
(the computation is somewhat tedious).
using Eq. 14 and 16
(the computation is somewhat tedious).