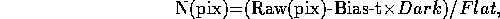
In contrast to stars, galaxies appear as extended objects on the sky and are therefore best observed using two-dimensional detectors instead of photometers. Photographic plates have dominated this field of astronomy until 15 years ago, when CCDs (Charged Coupled Devices, see Kitchin 1984) appeared on the market . CCDs are matrix detectors with a linear response in a wide intensity range, with a high quantum efficiency between 3500 Å and 9000 Å. CCDs are mounted at the focal plane of the telescope and convert the photons coming from the galaxies (and the sky) into electrons in a proportional way. They are therefore the best-suited instruments for galaxy photometry in the visible.
Raw CCD data as taken from the telescope must be corrected following some standard steps. The so-called ``bias'', a constant charge offset, present to avoid negative counts, must be subtracted. The thermic current increasing linearly with time (the ``dark current'') must be estimated and, if large, subtracted from the data. All of the bias (and dark current) subtracted frames must be divided by the pattern of the small pixel-to-pixel sensitivity variations (the ``flat field''). All of these corrections have been already applied to the data you are going to use:
where t is the exposure time and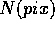 
are the counts per pixel
you find on the frames. The error associated with 
, 
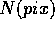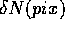, can be estimated as follows. The noise contributions due to
dark subtraction and flat fielding can be ignored, because the dark
current is usually very small and the flat fielding has a very high
signal to noise ratio. At low count levels the dominant source of
noise is the read-out noise RON, due to the electronics which
read the CCD. The RON can be determined from the rms of the bias
frame. Finally, one has the Poisson contribution or shot noise,
expected from the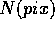 
detected photons, 
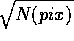. Combining
these last two sources of noise one finds:
CCDs are normally used in combination with filters, to select the appropriate range of wavelengths to be observed. Filters can be grouped into wide, intermediate and narrow ``band'' systems according to the widths of their transmission curves. Wide band filters typically have bandwidths of around 1000 Å, intermediate band filters range from 100 to 500 Å, while narrow band filters range from 0.5 to 100 Å. The CCD frames of this exercise have been taken with R and B filters. The R band filter has a central wavelength of approximately 6000 Å with a bandwidth of 1500 Å. The B band filter is centered on 4500 Å with a bandwidth of 1000 Å .
Finally, let us recall some of the usual words of the extragalactic jargon we will need in the next sections. The absolute flux F or absolute luminosity L (the two words are synonyms) of a source is the number of photons (in a given wavelenght interval) per second coming from it when its distance is 10 pc. The apparent flux f or apparent luminosity of a source is the number of photons (in a given wavelenght interval) per second coming from it. If D is the distance of the source in pc, then:
The instrumental flux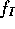 
is the number of photons (in a given
wavelenght interval) detected from a source in one second. One has:
where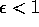 
is the total efficiency of the system (atmosphere,
telescope optics, detector).
Galaxies are extended
sources, so one introduces the concept of surface flux I,
which is the flux coming from an area of a squared arcsec of the
object in one second. Surface fluxes are distance-independent
quantities, because the area scales as the square of the distance, as
the flux does (see Eq. 3). Instrumental surface
fluxes are given as instrumental fluxes per pixel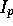 
.
In Eq. 1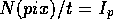 
(where t is the exposure time in seconds)
is then the instrumental flux per pixel coming from the
portion of the sky imaged on that pixel. The conversion of
the instrumental surface fluxes into
surface fluxes involves 
(see Eq. 4)
and the scale of the telescope. If one pixel is equivalent to
p arcsec, then one has:
Astronomers quote luminosities and surface luminosities using magnitudes:
where now M is the absolute magnitude of the object of absolute flux F. The relation between absolute and apparent magnitude m follows from Eq. 3:
where D is given in Mpc. Surface luminosities quoted in magnitudes
per square arcsec are called surface brightnesses SB.
Finally, it is convenient to convert absolute luminosities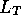 
of galaxies in
units of the absolute luminosity of the sun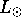 
.
If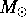 
is the absolute magnitude of the sun, and 
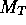the
absolute magnitude of a galaxy, then one has:
