The (apparent) integrated flux inside an aperture of radius R as a function of R is called curve of growth and is given by:
where I is the circularly averaged surface brightness of the galaxy
under study. When R becomes very large, Eq. 16 asymptotically
approaches the total (apparent) luminosity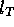 
of the galaxy.
The total (apparent) magnitude 
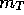is therefore:
For Eq. 14 one finds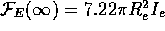 
, while
for Eq. 15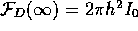 
. One defines the
half-luminosity or effective radius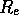 
as the radius where:
A related quantity is the average effective
surface luminosity, or the average surface luminosity inside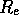 
:
For the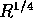 
law one therefore finds 
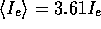. The related
surface brightness is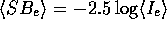 
. Note also the
(somewhat confusing) notation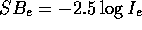 
.
Figure 8 shows Eq. 16 for the cases of the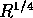 
law,
exponential profile and Bulge+Disk case. Note how different the profiles are:
you find only 85 % of the flux inside 4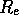
for the 
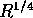law,
but 99 % for the exponential. Measuring total magnitudes and half-luminosity
radii of galaxies involves therefore some degree of extrapolation.
The simplest way to get a first estimate of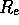 
and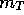 
is to
start from the outermost available data point of the curve of growth expressed
in magnitudes,
say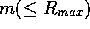 
, and find out the radius 
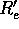where
Figure 9 shows the theoretical
relation between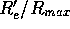 
and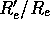 
, from which one can
derive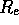 
. Finally one gets:
Please note the signs in Eq. 20 and Eq. 21.
A more precise method involves the all curve of growth. The plot of Fig.
10 shows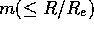 
as a function of 
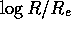. This is a
so-called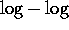 
plot: the shapes of the plotted
curves do not depend on the scale you used to normalize R or the
total fluxes. Plotting 
as a function of 
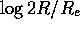would
result in the same curves shifted by 0.301 to the right. Plotting
the curves of growth normalized to 2 instead of 1 would result in the
same curves shifted by 0.75 to the top.
Therefore, you can superimpose Fig. 10
to the observed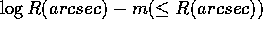 
profile and shift it
both in the x and in the y direction until
the best match between observed data and theoretical
curves are found. Only data points at radii larger than 3 arcsec should
be taken into account in this procedure, because of seeing
(see Section 2.3). Looking at where the position of 
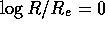of
Fig. 10 happens to be on the x axis of the observed plot
you derive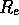 
in arcsec. Looking at where the position of 
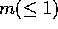of
Fig. 10 is on the y axis of the observed plot will give you
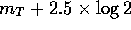of the galaxy.
