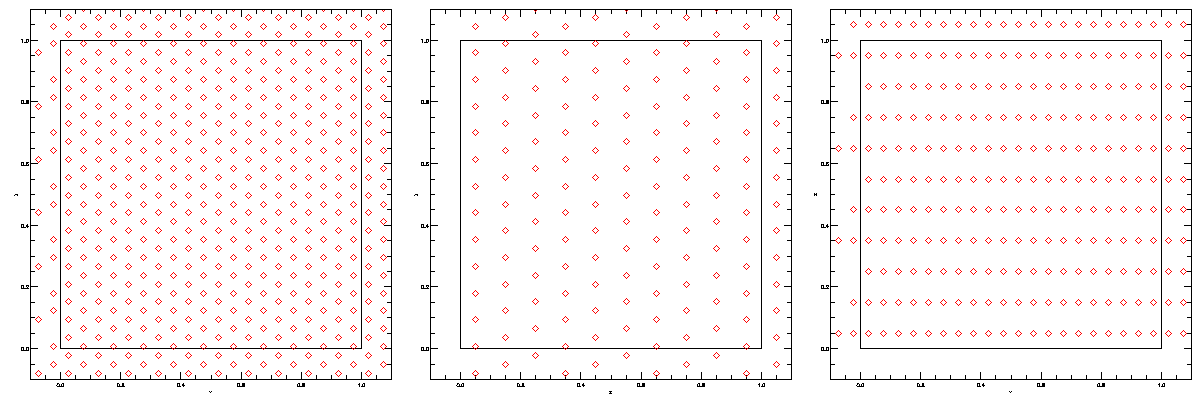
Start with this picture:
 taken from this paper (figure 1) and think about:
taken from this paper (figure 1) and think about:As discussed in the Lecture, kernel density estimates are the key pillar of smoothed particle hydrodynamics
(for an general overview on density estimations, see this
survey of existing methods).
Kernel density estimators are used to smooth a discretized distribution of tracer particles to obtain
continuous fields needed in hydrodynamics. Therefore it is important to understand the intrinsic properties
of such kernel density estimators.
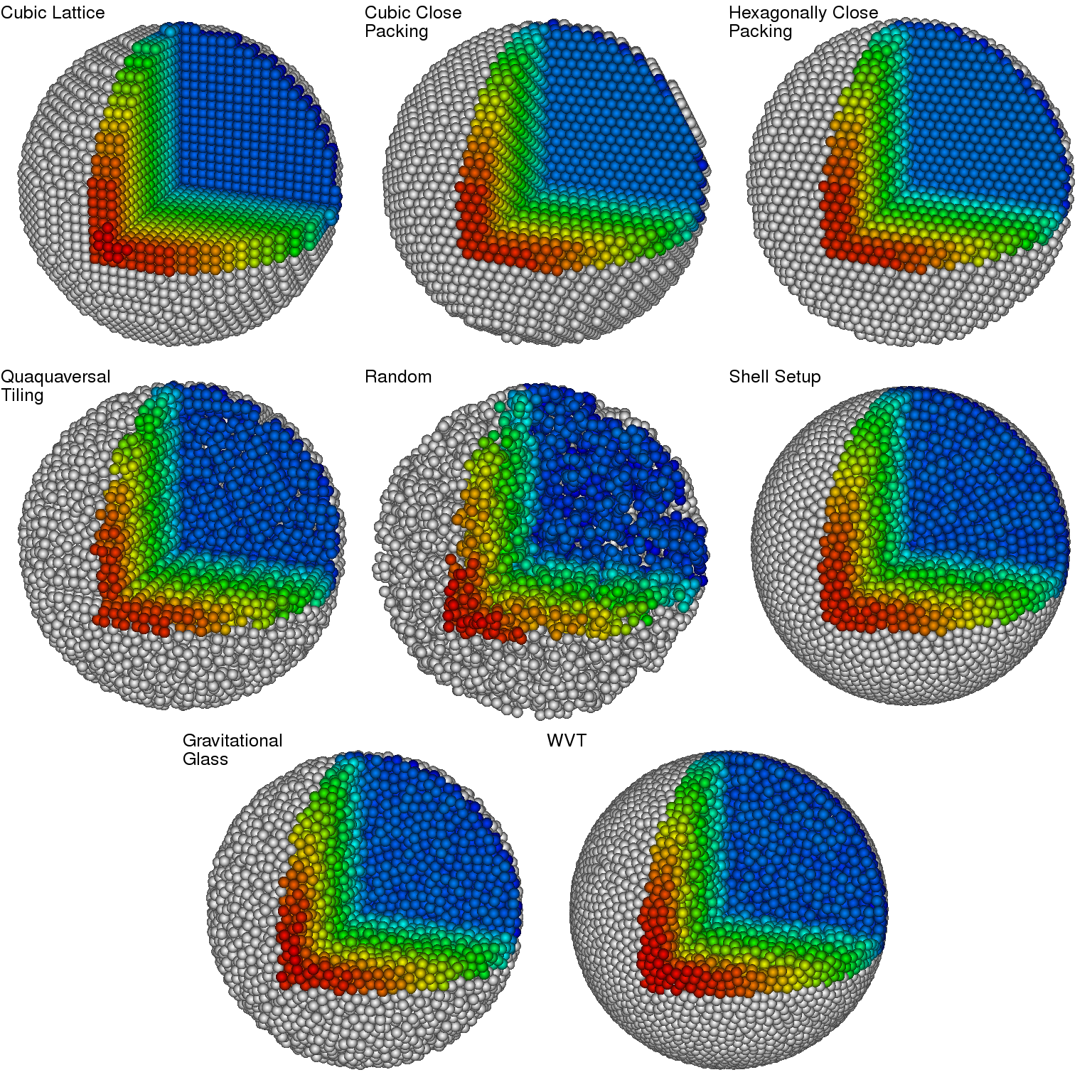
Start with this picture:
 taken from this paper (figure 1) and think about:
taken from this paper (figure 1) and think about:
The global properties of kernels have a significant impact on the performance of SPH. Make yourself familiar with some common choices of kernels (especially the spline and Wendland ones), as summarized in table 1 and figure 1 of this article.
You can start from the configuration of the code as obtained in T0b and collect some different particle distributions.
cp $HOME/Hydro/glass_10x10x10 .
setup_grid from T0b Step 3c
and modify it so that you get random positions of particles within the box.
You can now run the program using different kernels and different neighbor numbers.
Keep in mind that you do not need to run the simulation for a very long time,
basically you just need one output file.
So set the TimeMax as well as the TimeBetSnapshot parameter
in the box.param file to 0.5.
Every setup/combination of kernel, number of neighbors, and initial particle distribution
is an independent simulation you need to perform.
To do so, you can:
Config.sh file.
Choices are STANDARD_KERNEL (i.e., the standard, Cubic Spline kernel),
alternatively you can set QUINTIC_KERNEL,
WENDLAND_C2_KERNEL,
WENDLAND_C4_KERNEL, or
WENDLAND_C6_KERNEL in the
Config.sh file to select different kernels.
Only one of the above settings can be set.
Do not forget to re-compile after changing the kernel.
DesNumNgb parameter in the
box.param file, and re-run the simulation.
InitCondFile parameter in the box.param file to the
names of the different distributions and re-run the simulation.
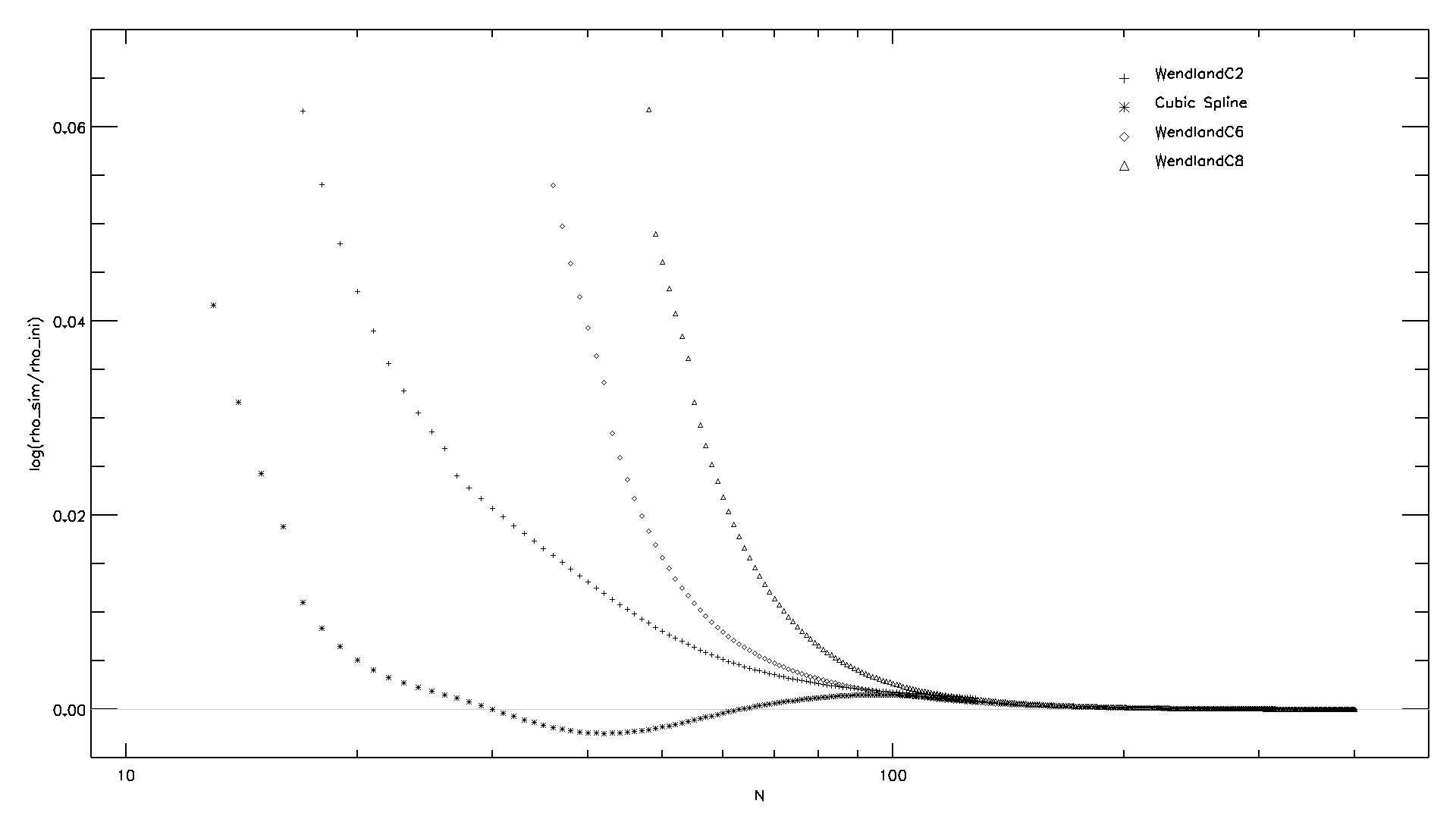
Now you can compare the resulting densities for the different simulations you produced.
You can read the density ("RHO ") for all particles within the different
simulations and compute the mean and the standard deviation, compared to the true density
used to create the initial conditions.
You can do this step by step:
Goal of this tutorial is that you learn better how to change the setup of the simulation and parameters.
What do you have to change to get only one output for each simulations?
Can you create a script to run the test with varying parameters?
How to produce a plot with multiple lines from different simulations?
How to produce one graph from the result of different simulations?
cp $HOME/Hydro/grid_10x10x10 .BoxSize 1 in the parameter file!
cp $HOME/Hydro/packed_12x12x12 .BoxSize 1 in the parameter file!
cp $HOME/Hydro/glass_10x10x10 .BoxSize 1 in the parameter file!
python3 print_values.pyUpdated 2024-11-12
idl -e show_kernels
ifx -g -traceback -check all -fpe0 -o meandensity meandensity.f90
bash runsims
gnuplot meandensity.plt
gv meandensity.ps
gnuplot density.plt
close_packed_lattice_new.pro in IDL