!DOCTYPE HTML PUBLIC "-//W3O//DTD W3 HTML 2.0//EN">
Planetarische Nebel als
<P>
,,Photonentransformatoren``



Next: Versuchsdurchführung
Up: No Title
Previous: Physikalische Grundgedanken
In ähnlicher Weise wie ein Fernsehapparat ein Bildschirm für
unsichtbare Elektronenstrahlen ist, ist der Planetarische Nebel
ein Bildschirm für die UV-Photonen seines Zentralsternes. Diese
Aussage wird deutlich, wenn man den Prozeß, dem
Planetarische Nebel unterliegen, im Detail betrachtet.
Der grundlegende Prozeß besteht darin, daß der Nebel nicht
beobachtbare Lyman-Quanten des Zentralsternes absorbiert (führt
zur Photoionisation) und in Folge von Rekombination und darauf
folgender spontaner Emission beobachtbare Quanten emittiert.
Dabei entspricht im zeitlichen Mittel die Anzahl der
Ionisationen der Summe der Rekombinationen. Dieser Sachverhalt wird
mit dem Begriff Ionisationsgleichgewicht beschrieben. Der Nebel
fungiert gleichsam als Photonen-,,Transformator``.
Weiterhin geht man davon aus, daß der Nebel wegen seiner gro
geometrischen Ausdehnung im Lyman-Kontinuum optisch dick ist
und folglich alle vom Zentralstern emittierten ionisierenden
Photonen absorbiert.
Dies ist das Kernstück der hier verwendeten Theorie:
Pro Zeiteinheit entspricht die Anzahl der ionisierenden Photonen
der Zahl der Ionisationen und diese wiederum der Zahl der
Rekombinationen.
Mathematisch lä sich dieser Sachverhalt wie folgt darstellen:
Sei 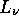 die Leuchtkraft des Sternes bei der Frequenz
die Leuchtkraft des Sternes bei der Frequenz  in erg/s/Hz. Die Anzahl der ionisierenden Quanten erhält man
dann, indem man
in erg/s/Hz. Die Anzahl der ionisierenden Quanten erhält man
dann, indem man 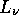 durch ein Quant der Energie
durch ein Quant der Energie 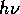 teilt
und über alle Frequenzen jenseits der Ionisationskante
(hier: Lyman-Kante für H oder He) integriert.
teilt
und über alle Frequenzen jenseits der Ionisationskante
(hier: Lyman-Kante für H oder He) integriert.
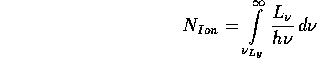
Die Anzahl der Rekombinationen hängt von der Elektronenzahldichte
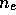 , der Protonenzahldichte
, der Protonenzahldichte 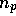 und dem totalen
Rekombinationskoeffizienten
abzüglich der Rekombination zum Grundzustand,
und dem totalen
Rekombinationskoeffizienten
abzüglich der Rekombination zum Grundzustand, 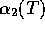 , ab:
, ab:
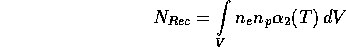
mit
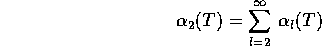
Mit 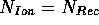 sieht man:
sieht man:

Die linke Seite von Gl.(1) kann man sich relativ einfach
beschaffen: das spektrale Verhalten des Zentralsterns ist im
Idealfall durch 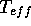 und
und 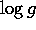 bestimmt und kann (im einfachsten
Fall) durch die Planck-Funktion
bestimmt und kann (im einfachsten
Fall) durch die Planck-Funktion 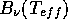 oder durch
eine Modellatmosphäre
oder durch
eine Modellatmosphäre 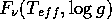 beschrieben werden.
Wenn es gelingt, die rechte Seite von Gl.(1) zu
berechnen, kann man durch einen einfachen Vergleich mit einem dieser
Modelle die Effektivtemperatur des Zentralsterns bestimmen.
beschrieben werden.
Wenn es gelingt, die rechte Seite von Gl.(1) zu
berechnen, kann man durch einen einfachen Vergleich mit einem dieser
Modelle die Effektivtemperatur des Zentralsterns bestimmen.
Man benützt jetzt den ,,Bildschirmcharakter`` des Nebels und betrachtet
die beobachbare Grösse 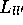 , mit
, mit

die die insgesamt emittierte Leuchtkraft einer bestimmten
Emissionslinie vom Niveau l nach 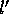 (z.B.
(z.B. 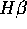 , l=4,
, l=4, 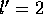 )
beschreibt.
)
beschreibt. 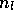 ist die Besetzungszahl des oberen Niveaus der
Linie,
ist die Besetzungszahl des oberen Niveaus der
Linie, 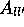 der Einsteinkoeffizient der spontanen Emission.
Man teilt nun diese Grösse durch Gl.(1) und bekommt:
der Einsteinkoeffizient der spontanen Emission.
Man teilt nun diese Grösse durch Gl.(1) und bekommt:
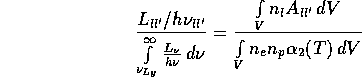
In der sogenannten ,,on the spot approximation`` nimmt man
an, daß
die Gleichung nicht nur über den ganzen Nebel sondern auch ,,lokal``
erfüllt ist, und man kann schreiben:

Gl.(3) enthält nun die bemerkenswerte Aussage, daß die
Zahl der Photonen, die der Nebel in einer bestimmten Spektrallinie
emittiert, proportional zur Zahl der Photonen ist, die der Zentralstern
im Lyman-Kontinuum
emittiert ( Zanstra, 1931, Publ.Dom.Astrophys.Obs. 4,209).
Mit der Beziehung:
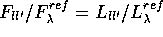 (Die mit F bezeichneten Grösse beschreiben beobachtete
Flüsse, ,, ref`` bezieht sich auf eine beliebige
Referenzfrequenz
in einen Bereich ohne Emissionslinien, d.h. man sieht ausschliessich
die stellare Strahlung. Im visuellen Bereich verwendet
man i.a.
(Die mit F bezeichneten Grösse beschreiben beobachtete
Flüsse, ,, ref`` bezieht sich auf eine beliebige
Referenzfrequenz
in einen Bereich ohne Emissionslinien, d.h. man sieht ausschliessich
die stellare Strahlung. Im visuellen Bereich verwendet
man i.a. 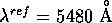 .
.  bezieht
sich auf
die gewählte Emissionslinie, üblicherweise H
bezieht
sich auf
die gewählte Emissionslinie, üblicherweise H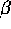 oder He4686.)
kann man Gl.(3) zweckmä ssig umschreiben:
oder He4686.)
kann man Gl.(3) zweckmä ssig umschreiben:
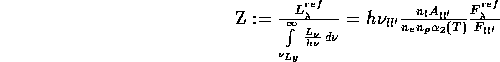
Z definiert dabei das sogenannte ,,Zanstra-Verhältnis``.
Die linke Seite kann nun zur Bestimmung der Effektivtemperatur
des Zentralsterns verwendet werden, entweder approximativ durch
die Planckfunktion oder besser (?) mit dem Ergebnis einer
Modellatmosphäre:
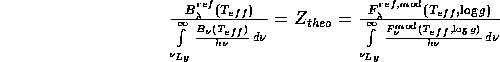
Trotz dieser nicht tricklosen Vorgehensweise
( Harman und Seaton, 1966,
MNRAS 132,15 für die speziell Interessierten) verbleibt uns
das Problem, die rechte Seite von Gl.(3) zu berechnen.
Dem wollen wir uns jetzt zuwenden.
Die eigentliche Schwierigkeit stellt dabei die Berechnung der
Besetzungszahlen dar. In Gl.(4) will man die Besetzungszahl
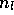 als Funktion der Dichten
als Funktion der Dichten 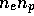 ausdrücken.
Man benötigt dafür die Gleichungen des
statistischen Gleichgewichts, die aber für Planetarische Nebel
wegen des extremen non-LTE (s.o.) besonders einfach sind. Zu
berücksichtigen sind lediglich die Rekombination und die
Kaskadierung zum Grundzustand.
ausdrücken.
Man benötigt dafür die Gleichungen des
statistischen Gleichgewichts, die aber für Planetarische Nebel
wegen des extremen non-LTE (s.o.) besonders einfach sind. Zu
berücksichtigen sind lediglich die Rekombination und die
Kaskadierung zum Grundzustand.
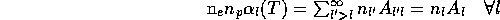
wobei

Der physikalische Sachverhalt wird klarer, wenn man die
Wahrscheinlichkeit 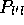 einführt, mit der ein direkter
Strahlungsübergang von
einführt, mit der ein direkter
Strahlungsübergang von 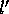 nach l erfolgt:
nach l erfolgt:

Damit kann man Gl.(6) auf folgende Weise anschaulicher
schreiben:
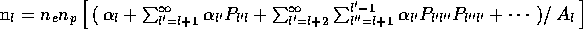
In der dargestellten Reihenfolge beschreiben die einzelnen Terme in
den eckigen Klammern die Population des l-ten Levels durch:
-
direkte Rekombination nach l
-
Rekombination zu einem höheren Niveau gefolgt von einem direkten
Strahlungsübergang nach l
-
Rekombination zu einem höheren Niveau und Kaskadierung nach l
über einen Zwischenzustand
-
 über zwei Zwischenzustände
über zwei Zwischenzustände 
Die eckige Klammer kann somit für hydrogenische Atome berechnet
und tabelliert werden (s.Tab.1). Die Tabellierung ist
so gehalten, daß die Ladungsabhängigkeit 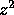 in der Temperatur
T des Plasmas bereits berücksichtigt ist.
in der Temperatur
T des Plasmas bereits berücksichtigt ist.

wobei gilt: 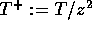 .
Setzt man dies in Gl.(4) ein, bekommt man sofort:
.
Setzt man dies in Gl.(4) ein, bekommt man sofort:

Die 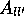 sind in Tab.2 für die wichtigsten H-- und
He--Linien angegeben.
Es verbleibt noch die erheblich mühsamere Berechnung der
Rekombinationskoeffizienten
sind in Tab.2 für die wichtigsten H-- und
He--Linien angegeben.
Es verbleibt noch die erheblich mühsamere Berechnung der
Rekombinationskoeffizienten 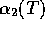 ( Seaton, 1959, MNRAS 119,81), die aber durch folgende Formel
gut (zumindest für H und HeII) approximiert werden können:
( Seaton, 1959, MNRAS 119,81), die aber durch folgende Formel
gut (zumindest für H und HeII) approximiert werden können:
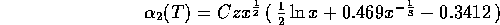
Hierbei sind:
z die Kernladungszahl
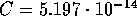
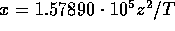
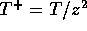
Tabelle 1: Werte für 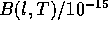

Tabelle 2: Werte für
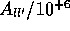 --
-- 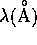 in Klammern
in Klammern



Next: Versuchsdurchführung
Up: No Title
Previous: Physikalische Grundgedanken
Roberto Saglia
Tue Sep 16 15:53:04 MET DST 1997
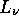 die Leuchtkraft des Sternes bei der Frequenz
die Leuchtkraft des Sternes bei der Frequenz  in erg/s/Hz. Die Anzahl der ionisierenden Quanten erhält man
dann, indem man
in erg/s/Hz. Die Anzahl der ionisierenden Quanten erhält man
dann, indem man 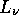 durch ein Quant der Energie
durch ein Quant der Energie 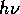 teilt
und über alle Frequenzen jenseits der Ionisationskante
(hier: Lyman-Kante für H oder He) integriert.
teilt
und über alle Frequenzen jenseits der Ionisationskante
(hier: Lyman-Kante für H oder He) integriert.
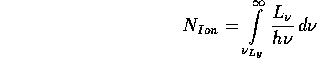
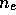 , der Protonenzahldichte
, der Protonenzahldichte 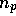 und dem totalen
Rekombinationskoeffizienten
abzüglich der Rekombination zum Grundzustand,
und dem totalen
Rekombinationskoeffizienten
abzüglich der Rekombination zum Grundzustand, 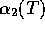 , ab:
, ab:
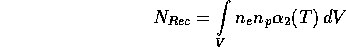
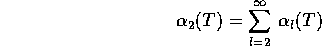
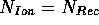 sieht man:
sieht man:

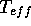 und
und  bestimmt und kann (im einfachsten
Fall) durch die Planck-Funktion
bestimmt und kann (im einfachsten
Fall) durch die Planck-Funktion 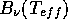 oder durch
eine Modellatmosphäre
oder durch
eine Modellatmosphäre 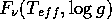 beschrieben werden.
Wenn es gelingt, die rechte Seite von Gl.(
beschrieben werden.
Wenn es gelingt, die rechte Seite von Gl.(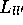 , mit
, mit

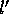 (z.B.
(z.B. 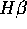 , l=4,
, l=4, 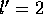 )
beschreibt.
)
beschreibt. 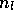 ist die Besetzungszahl des oberen Niveaus der
Linie,
ist die Besetzungszahl des oberen Niveaus der
Linie, 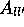 der Einsteinkoeffizient der spontanen Emission.
Man teilt nun diese Grösse durch Gl.(
der Einsteinkoeffizient der spontanen Emission.
Man teilt nun diese Grösse durch Gl.(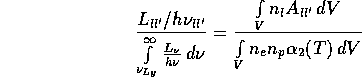

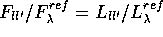 (Die mit F bezeichneten Grösse beschreiben beobachtete
Flüsse, ,, ref`` bezieht sich auf eine beliebige
Referenzfrequenz
in einen Bereich ohne Emissionslinien, d.h. man sieht ausschliessich
die stellare Strahlung. Im visuellen Bereich verwendet
man i.a.
(Die mit F bezeichneten Grösse beschreiben beobachtete
Flüsse, ,, ref`` bezieht sich auf eine beliebige
Referenzfrequenz
in einen Bereich ohne Emissionslinien, d.h. man sieht ausschliessich
die stellare Strahlung. Im visuellen Bereich verwendet
man i.a. 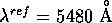 .
.  bezieht
sich auf
die gewählte Emissionslinie, üblicherweise H
bezieht
sich auf
die gewählte Emissionslinie, üblicherweise H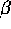 oder He4686.)
kann man Gl.(
oder He4686.)
kann man Gl.(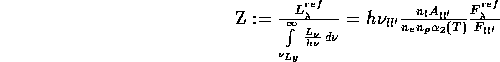
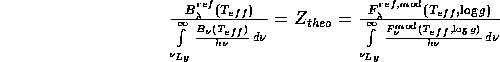
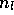 als Funktion der Dichten
als Funktion der Dichten 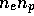 ausdrücken.
Man benötigt dafür die Gleichungen des
statistischen Gleichgewichts, die aber für Planetarische Nebel
wegen des extremen non-LTE (s.o.) besonders einfach sind. Zu
berücksichtigen sind lediglich die Rekombination und die
Kaskadierung zum Grundzustand.
ausdrücken.
Man benötigt dafür die Gleichungen des
statistischen Gleichgewichts, die aber für Planetarische Nebel
wegen des extremen non-LTE (s.o.) besonders einfach sind. Zu
berücksichtigen sind lediglich die Rekombination und die
Kaskadierung zum Grundzustand.
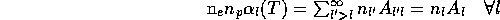

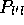 einführt, mit der ein direkter
Strahlungsübergang von
einführt, mit der ein direkter
Strahlungsübergang von 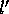 nach l erfolgt:
nach l erfolgt:

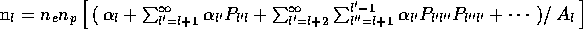
 über zwei Zwischenzustände
über zwei Zwischenzustände 
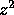 in der Temperatur
T des Plasmas bereits berücksichtigt ist.
in der Temperatur
T des Plasmas bereits berücksichtigt ist.

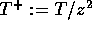 .
Setzt man dies in Gl.(
.
Setzt man dies in Gl.(
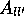 sind in Tab.2 für die wichtigsten H-- und
He--Linien angegeben.
Es verbleibt noch die erheblich mühsamere Berechnung der
Rekombinationskoeffizienten
sind in Tab.2 für die wichtigsten H-- und
He--Linien angegeben.
Es verbleibt noch die erheblich mühsamere Berechnung der
Rekombinationskoeffizienten 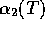 ( Seaton, 1959, MNRAS 119,81), die aber durch folgende Formel
gut (zumindest für H und HeII) approximiert werden können:
( Seaton, 1959, MNRAS 119,81), die aber durch folgende Formel
gut (zumindest für H und HeII) approximiert werden können:
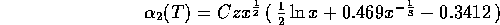
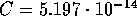
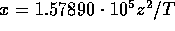
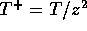
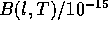
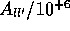 --
-- 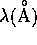 in Klammern
in Klammern