
Digital and Cray use the number of bytes as the KIND-parameter. Digital permits the values 1, 4, 8 and 16 for logical variables (with the same result as for the default value 4), the values 2, 4 and 8 for integers, the values 4, 8 and 16 for floating point values, and the values 4 and 8 for complex values. The name quad for the case KIND=16 is my own! Also the names int15, int31, and int63 are mine.
LOGICAL Default byte word
KIND number = 4 1 4
LOGICAL Default double quad
KIND number = 4 8 16
INTEGER int15 int31 int63
KIND number = 2 4 8
digits = 15 31 63
radix = 2 2 2
range = 4 9 18
huge = 32767 2147483647 9223372036854775807
bit_size = 16 32 64
REAL single double quad
KIND number = 4 8 16
digits = 24 53 113
maxexponent = 128 1024 16384
minexponent = -125 -1021 -16381
precision = 6 15 33
radix = 2 2 2
range = 37 307 4931
epsilon = 0.11920929E-06 0.22204460E-15 0.19259299E-33
tiny = 0.11754944E-37 0.22250739-307 0.33621031-4931
huge = 0.34028235E+39 0.17976931+309 0.11897315+4933
COMPLEX single double
KIND number = 4 8
precision = 6 15
range = 37 307
The source code in fix form should have the extension .f, .for or .FOR, while the source code in free form should have the extension .f90.
Note especially that using these switches it is possible to choose different sizes (number of bits) for integers (with integer_size), single precision values (with real_size) and double precision numbers (with double_size) to the desired bit-length (number of bytes). Since the Alpha processor is a 64-bit processor it is recommended to use 64 bits for the floating point numbers, that is to use the extension -real_size 64 or simpler -r8.
-c Only compilation (no linking)
-C Index check
-double_size 64 (default)
-double_size 128 (double precision becomes quad)
-f fixed The old form of the source code (fix form)
-f free The new form of the source code (free form)
-g Creates debug information
-i Selects the integer length. Use
-i2 or integer_size 16
-i4 or integer_size 32 (default)
-i8 or integer_size 64
-Idir Fortran 90 looks for files for the
Fortran INCLUDE statement in this directory
-l Linking of libraries
-o Naming the final program
-O Optimization
-pg Generates execution profile for gprof
-real_size 32 (default)
-real_size 64 or -r8
-real_size 128 or -r16
-u Implies IMPLICIT NONE without an explicit statement
in each program unit
-v Comments how the compilation proceeds
-V Writes the source code with the extension .l
-version Gives the version number of the compiler
-vms Gives certain VAX VMS properties (does not switch
to VAX-arithmetics)
-w Suppresses warnings
My tests indicate that it follows IEEE 754 correctly (single and double precision, higher precisions are not yet standardized).
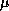 in
the program EPSILON. This program, which is written in normal single
precision, is in the file
epsilon.f90. It has been run
in all the three possible precisions.
in
the program EPSILON. This program, which is written in normal single
precision, is in the file
epsilon.f90. It has been run
in all the three possible precisions.
% f90 epsilon.f % a.out mu = 5.9604645E-08 % f90 -r8 epsilon.f % a.out mu = 1.110223024625157E-016 % f90 -r16 epsilon.f % a.out mu = 9.629649721936179265279889712924637E-0035 %
The second example is summation forwards and backwards, with the program SUMMATION. This program is in the file sum.f90. Its mathematical/numerical task is to show that summation starting with the smallest values gives the most accurate result. At one run this program handles all three possible precisions.
Single and double precision are specified in the ordinary way with REAL and DOUBLE PRECISION, respectively, while for quad precision we use the possibility of introducing a user-selected precision, which is given the name QUAD. The definition uses the function SELECTED_REAL_KIND in order to obtain a suitable (KIND-number), see chapter 13.
% f90 sum.f90 % a.out How many numbers do you wish to add? 1e6 Do you want to add forwards (F) or backwards (B)? f Summation forwards of 1000000 numbers. The sum in single precision = 1.644725 The sum in double precision = 1.64493306684877 The sum in quad precision = 1.64493306684872643630574849997952 % a.out How many numbers do you wish to add? 1e6 Do you want to add forwards (F) or backwards (B)? b Summation backwards of 1000000 numbers. The sum in single precision = 1.644933 The sum in double precision = 1.64493306684873 The sum in quad precision = 1.64493306684872643630574849997939 %It is easy to switch the double precision to quad precision through compiling the program sum.f90 with
% f90 -double_size 128 sum.f90but it is not possible to switch the single precision, since the notation 0.0_QUAD then gives a compilation error. If we replace the offending expression with 0.0 (and the corresponding substitutions for any other constants) we can use
% f90 -r8 sum.f90to obtain that both single and double precision are treated as double precision, while quad precision remains unaffected. With
% f90 -r16 sum.f90all calculations are done in the quad precision.