Zum Vergleich: Auch die Sonne weist einen Wind auf, den berühmt-berüchtigten Sonnenwind, der
allerdings ganz anders "funktioniert" als die hier behandelten Winde heißer Sterne. Dies
sieht man schon daran, daß die Massenverlustrate der Sonne erheblich geringer ist als die oben genannten
Werte.
Mdot (Sonne): ca. 10-14 Msun/a (entsprechend einer "Ostseemasse" pro Jahr).
1.2.2 Endgeschwindigkeit
Weit entfernt von der Sternoberfläche erreicht die Materieabströmung ihre maximale Geschwindigkeit, die
danach - in Abwesenheit äußerer Kräfte - konstant bleibt und deshalb Endgeschwindigkeit v¥ genannt wird (vgl. das Erste Newtonsche Axiom: "In Abwesenheit
äußerer Kräfte verharrt ein Körper entweder im Zustand der Ruhe oder der geradlinig gleichförmigen Bewegung")
"Beobachtete" Werte dieser Endgeschwindigkeiten zeigen, daß sie die lokale Schallgeschwindigkeit
um ein Vielfaches (bis zu einem Faktor 100) übersteigen.
- Typische Werte der Endgeschwindigkeit liegen im Bereich 200 km/s ... 3000 km/s.
- Die Schallgeschwindigkeiten bei diesen Sternen variiert von ca. 10 km/s ... 30 km/s.
- Zum Vergleich: Die Schallgeschwindigkeit auf der Erde ist um einiges geringer, sie liegt bei
0.3 km/s. (Was ist der Unterschied?)
1.3 Warum beschäftigen wir uns mit Sternwinden?
Einige Punkte, die die astrophysikalische Relevanz stellarer Winde aufzeigen.
1.3.1 Sternentwicklung
Lebensdauer heißer Sterne
- einige 106 Jahre; zum Vergleich - Lebensdauer der Sonne: ca. 7 ·109 Jahre
d.h., 1000 Generationen heißer Sterne pro einer Generation sonnenähnlicher Sterne.
Aufgrund der Höhe des Massenverlustes (Größenordnung 10-6
Msun/a) ist der Massenverlust
signifikant und beträgt einige Sonnenmassen (bei einer Masse des Sternes von 10 - 100
Sonnenmassen). Massenverlust hat eine entscheidende Bedeutung für die
und muß deshalb in
allen Phasen der Sternentwicklung bekannt sein, um korrekt berücksichtigt
werden zu können.
1.3.2 Galaxienentwicklung
- Im Inneren aller Sterne wird Energie durch Kernfusion ("Verschmelzung") erzeugt.
- Dadurch wird das Verhältnis der Elementhäufigkeiten verändert (gegenüber dem Ausgangsverhältnis
bei der "Geburt" des Sternes).
- Bei heißen Sterne ist davon hauptsächlich das Verhältnis
Wasserstoff : Helium : Kohlenstoff : Stickstoff : Sauerstoff
betroffen.
Durch den Massenverlust wird Material mit dieser veränderten Zusammensetzung der Elemente an die
stellare Umgebung abgegeben. Da heiße Sterne (fast) immer in Gruppen auftreten, verändert dieser Prozeß
die Elementhäufigkeiten im sog. interstellaren Medium und hat damit einen wichtigen Einfluß auf
die
1.3.3 Sternentstehung
- Wind = hochgradige Überschallströmung
prallt auf umgebendes Medium.
- Dies führt zur Entwicklung von Stoßfronten (analog zum Überschallknall) und
- zu lokalen Verdichtungen des umgebenden Mediums, die die "Geburt" neuer Sterne
auslösen.
1.3.4 Heiße Sterne als Entfernungsindikatoren
siehe Kap. 1.1.2 und "Die Windimpuls-Leuchtkraft-Relation"(Kap. 5.3)
1.3.5 Sternwinde als physikalisches Laboratorium
- Winde heißer Sterne werden durch den sog. Linienstrahlungsdruck verursacht und beschleunigt
(vgl. Kap. 2. und Kap. 5).
- Dieser Prozeß ist physikalisch äußerst interessant, läßt sich allerdings in Laboratorien auf
der Erde nicht oder nur unzureichend studieren.
- Durch Beobachtung und detaillierte Analyse der von diesen Sternen abgestrahlten Energieverteilung
läßt sich die Physik des Linienstrahlungsdrucks in situ studieren, d.h. wir können die Sternwinde
als
| PHYSIKALISCHES LABORATORIUM |
nutzen.
2 Der Beschleunigungsmechanismus der Sternwinde
In diesem Abschnitt stellen wir den physikalischen Mechanismus vor, der die Winde heißer Sterne initiiert
und beschleunigt. Der entsprechende Formalismus wird in Kap. 5 eingehend entwickelt. Die wesentlichen
Effekte werden in der folgenden Abbildung aufgezeigt.
- aus den tieferen Schichten der Atmosphäre, der sog. Photosphäre, werden Photonen
in einem großen Spektralbereich emittiert.
- Diese Photonen gelangen in den Wind und können ihren Impuls auf die dort vorhandenen Ionen
übertragen. Dies geschieht in einem zweistufigen Prozeß (vgl. den unteren Bereich der Abbildung)
- Photonen können immer dann von einem Ion (z.B. Kohlenstoff, Stickstoff, Silizium, Eisen,
Nickel etc., die sich alle in den Sternatmosphären befinden) absorbiert werden, wenn ihre Energie
gerade derjenigen Energie entspricht, die benötigt wird, um ein Elektron der Ionen anzuregen.
- Bei diesem Prozeß wird nicht nur die Energie des Photons in Anregungsenergie umgewandelt
(das Photon ist damit zerstört), sondern auch Impuls auf das Ion übertragen. Da Photonen hauptsächlich
aus der Richtung des Sternes kommen, werden damit die Ionen im Mittel nach außen beschleunigt.
- Nach einer relativ kurzen Zeit, der sog. mittleren Lebensdauer (Größenordnung 10-8 Sekunden), "fällt" das Elektron entweder auf seinen Grundzustand
oder eine andere, niederenergetische Bahn, zurück.
- Bei diesem Übergang des Elektrons wird die freiwerdende Energie durch die Emission eines
"neuen" Photons kompensiert.
- Der Impuls des emittierten Photons muß vom emittierenden Ion kompensiert werden, d.h. das
Ion wird in entgegengesetzter Richtung des Photons beschleunigt.
- Die Gesamtbeschleunigung des Ions aufgrund von Absorption und Emission ist die Vektorsumme
der beiden Beschleunigungen.
- Da die Richtung, in die das Photon emittiert wird, zufällig ist, mitteln sich (bei vielen
Emissionsakten) die einzelnen "Emissionsbeschleunigungen" heraus und es bleibt praktisch
nur die auswärtsgerichte "Absorptionsbeschleunigung" übrig.
- Die nach außen beschleunigten Ionen geben letztendlich ihren Impuls durch Stöße auf das Restplasma
(hauptsächlich Wasserstoff) ab, und der Wind wird insgesamt nach außen beschleunigt!
- Da das photosphärische Strahlungsfeld bei heißen Sternen hoch und auch die Anzahl der möglichen
Übergänge der Elektronen groß ist, lassen sich die beobachteten Massenverlustraten und Endgeschwindigkeiten
zwanglos erklären. (Bei kühlen Sternen ist das Strahlungsfeld zu schwach, um über den hier geschilderten
Prozeß einen Wind zu initiieren.)
Da es sich bei obigen Übergängen der Elektronen um Linienübergänge handelt, spricht man von einer
Windbeschleunigung aufgrund von
3 UV Beobachtungen heißer Sterne
Im folgenden zeigen wir typische Spektren heißer Sterne, die im UV-Bereich aufgenommen wurden.
Dabei handelt es sich um den Energiebereich zwischen 1150 ... 1850 Å.
Die erste Serie umfaßt dabei Aufnahmen des Satelliten IUE ("International Ultraviolet Explorer"),
einem der für die Winddiagnostik heißer Sterne bislang wichtigsten Instrumente, und zeigt galaktische
Objekte.
Die zweite Serie veranschaulicht UV-Spektren des neueren und in der Öffentlichkeit bekannteren HST
("Hubble Space Telescope") für Sterne in der KLEINEN UND GROSSEN MAGELLANSCHEN WOLKE
(SMC und LMC), das sind relativ kleine und junge Nachbargalaxien unserer Milchstraße, die am Südhimmel
zu finden sind.
Dargestellt ist in beiden Serien das beobachtete Spektrum als Funktion der Wellenlänge, wobei diese Verteilung
auf die von der Photosphäre abgestrahlte kontinuierliche Energieverteilung normiert ist. Diese liegt
in den Abbildungen in der Höhe "1".
Man beachte insbesondere die breiten Linien bei
- ca. 1240 Å (N4+, vierfach ionisierter Stickstoff)
- ca. 1400 Å (Si3+, dreifach ionisiertes Silizium)
- ca. 1550 Å (C3+, dreifach ionisierter Kohlenstoff)
- ca. 1720 Å (N3+, dreifach ionisierter Stickstoff)
die bis auf die letzte sog. Resonanzlinien darstellen, d.h. durch Übergänge des äußersten Elektrons
vom Grundzustand zum ersten angeregten Zustand und zurück verursacht werden. Zwei Linien der obigen Auswahl,
die des vierfach ionisierten Stickstoffs (= N v im astrophysikalischen Jargon) und die des dreifach ionisierten
Kohlenstoffs (C iv), sollen in diesem Praktikum von Ihnen analysiert werden, und zwar für eine umfassende
Stichprobe galaktischer O-Sterne.
Aufgrund ihrer Form bezeichnet man diese sehr breiten Linien als sog. "P-Cygni Linien". Diese
ermöglichen uns, wie im nächsten Abschnitt ausgeführt, einen großen Einblick in die Windphysik, da sie
vom gesamten Windbereich beeinflußt werden.
Die Vielzahl anderer Linien entsteht größtenteils in der unteren Atmosphäre (bei niedrigen Geschwindigkeiten)
und ist im Rahmen der hier vorgestellten Winddiagnostik von geringerem Interesse.
Bei den hier vorgestellten Sternen handelt es sich generell um Sterne des sog.
Spektraltyps
"O", d.h. um Sterne mit Oberflächentemperaturen
heißer als 30000 K. (O3 heißer als
47000 K).
Die der Leuchtkraftklasse nachfolgenden Bezeichnungen dienen der Kennzeichnung von Eigentümlichkeiten
der Spektren und sind an dieser Stelle von keinem weiteren Interesse.
Letztendlich sei noch die Bezeichnung der Sterne angesprochen. Diese orientieren sich am Verfasser
des jeweiligen Kataloges, worin sie aufgeführt sind (z.B. HD = Henry Draper) plus einer Nummer (oder
Koordinaten, wie im Sk (=Sanduleak)- Katalog), oder sie sind bzgl. der Region numeriert (in NEUSCHREIB:
nummeriert), in der sie sich finden, wie im Falle der NGC346-Sterne.
3.1 UV Spektren (IUE) von heißen Sternen in der Galaxis
Die hier vorgestellten IUE-Spektren wurden freundlicherweise von Dr. Ian Howarth und Dr. Raman Prinja
(beide University College, London) zur Verfügung gestellt. Massenverlustraten und Endgeschwindigkeiten
sind, wie schon angeprochen, im Rahmen des Praktikums zu bestimmen.
Figure 1: HD 93129A - O3 If*: "Schwerster Stern der Galaxis." Tef f = 50500 K, R*
= 20 Rsun, M = 130! Msun, Mdot = ?, v¥
= ?.
Figure 2: HD 66811 (z Pup) - O4 I(f): Dieser Stern (Südhimmel)
ist der Standardstern der Heißstern- und Windphysik! Tef f
= 42000 K, R* = 19 Rsun, M = 53 Msun,
Mdot = ?,v¥ = ?.
Figure 3: HD 13268 - O8 III: Sehr geringer Massenverlust! Tef
f = 35000 K, R* = 12 Rsun,
M = 16 Msun, Mdot = ?, v¥ = ?.
Figure 4: HD 30614 (a Cam) - O9.5 Ia: Ein anderer Paradestern,
diesmal am Nordhimmel ... Tef f
= 30000 K, R* = 29 Rsun, M = 31 Msun,
Mdot = ?, v¥ = ?.
3.2 UV Spektren (HST) von heißen Sternen in der SMC
Figure 5: NGC 346 #3 - O3 IIIf*: Tef f
= 55000 K, R* = 12 Rsun, M = 44 Msun,
Mdot = 2.3 ·10-6 Msun/a, v¥ = 2900 km/s.
Figure 6: NGC 346 #1 - O4 III(n)(f): Man vergleiche mit z Pup!
Tef f = 42000 K, R*
= 23 Rsun, M = 88 Msun, Mdot = 4.8 ·10-6
Msun/a, v¥
= 2600 km/s.
Figure 7: AV 232 - O7 Iaf+. Tef f
= 37500 K, R* = 29 Rsun, M = 62 Msun,
Mdot = 5.5 ·10-6 Msun/a, v¥ = 1400 km/s. Man beachte, daß die
Sterne der SMC niedrigere Endgeschwindigkeiten als analoge Sterne in der Galaxis haben.
3.3 UV Spektren (HST) von heißen Sternen in der LMC
Figure 8: Sk-67 211 - O3 III(f*): Tef f
= 60000 K, R* = 18 Rsun, M = 163 Msun,
Mdot = 10 ·10-6 Msun/a, v¥ = 3750 km/s (Geschwindigkeitsrekord!).
Figure 9: Melnick 42 - O3 If/WN: Der erste heiße Stern, der mit dem HST detailliert beobachtet
wurde. Tef f = 50500 K, Mdot = 35
·10-6 Msun/a,
v¥ = 3000 km/s (vgl. Titelbild). Der Radius dieses Sternes
soll im Praktikum bestimmt werden!
Figure 10: Sk-67 166 - O4 If+: Tef f
= 47500 K, R* = 19 Rsun, M = 62 Msun,
Mdot = 13 ·10-6 Msun/a, v¥ = 1900 km/s.
4 P Cygni Profile
4.1 Entstehung von P Cygni Profilen
Wie im vorhergehenden Abschnitt ausgeführt, erlauben die breiten, sog. "P Cygni Profile", die
bei heißen Sternen im UV beobachtet werden, einen tiefen Einblick in die physikalischen Bedingungen des
Sternwindes. (Diese Art eines Profiles wird deshalb so genannt, weil sie erstmalig im Spektrum des Sternes
P Cygni gefunden wurde.)
Da wir uns im nächsten Abschnitt ausführlich mit der Diagnostik dieser Profile beschäftigen werden,
soll an dieser Stelle kurz skizziert werden, wie sie zustandekommen.
Der zentrale Effekt, der hier zum Tragen kommt, ist der sog. Doppler-Effekt.
(Der Inhalt der nächsten beiden Absätze sollte eigentlich jedem Studenten der Naturwissenschaften klar
sein, wird hier aber trotzdem? angeführt.) Der Doppler-Effekt ist schon aus dem täglichen Leben bekannt,
wenn man sich vor Augen (besser vor Ohren) führt, was passiert, wenn sich ein Polizei- oder Krankenwagen
mit eingeschalteter Sirene einem am Randstein stehenden Zuschauer / Zuhörer nähert und dann wieder entfernt.
Zunächst hört man die Sirene mit relativ hohen Tönen, d.h. mit einer höheren Frequenz als derjenigen,
die der Fahrer in seinem Wagen hört oder die man hören würde, falls der Wagen stünde. Die Tonhöhe wird
dann schlagartig tiefer, wenn der Wagen den "Beobachter" passiert und sich von ihm entfernt.
Sie ist dann auch tiefer, als sie dem Fahrer erscheint. (Dieser hört natürlich immer die gleiche Frequenz.)
Den analogen Effekt - nun bezüglich der Frequenz der Lichtstrahlung - sieht ein Beobachter auf der Erde,
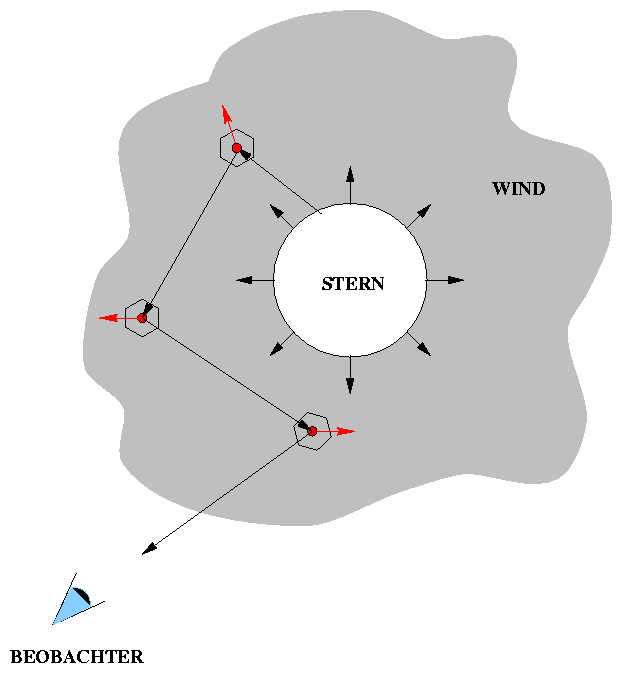
wenn er verschiedene Bereiche des Windes betrachtet (man vergleiche im weiteren die folgende Abbildung):
- Schaut er nämlich auf die ihm zugewandte Hälfte des Windes (Teil "A, B" vor
der hellen Trennungslinie), sieht er das Windmaterial auf sich zu kommen, und zwar, von innen nach
außen, mit anwachsender Geschwindigkeit:
- das äußerste Material kommt am schnellsten auf ihn zu (mit maximaler Geschwindigkeit v¥), so daß er diese Strahlung mit einer höheren Frequenz sieht, als sie
von den Ionen im Wind "gesehen" werden.
- das innerste Material hat eine Geschwindigkeit von nahezu Null bezüglich des Beobachters, d.h.,
dieser sieht die Strahlung bei gleicher Frequenz wie das Windmaterial.
- Schaut man nun auf das rückwärtige Material (Teil "C" hinter der hellen Linie), so
sieht man dieses, wie es sich vom Beobachter entfernt. Deshalb ist die beobachtete Frequenz
tiefer, d.h. liegt bei höherer Wellenlänge. Wieder sieht man im wesentlichen alle Geschwindigkeiten
von Null bis -v¥, wobei das "Minuszeichen"
daher rührt, daß sich das Material von einem weg bewegt.
Figure 11: Entstehung von P Cygni Profilen
Hat man diese Argumentation einmal verstanden, so läßt sich die spezielle Form eines P Cygni Profiles
folgendermaßen erkären:
- Betrachten wir zunächst den Absorptionsprozeß im Wind, d.h. die Anregung von Elektronen
durch die Strahlung des Sternes. Vergleichen wir mit dieser Strahlung (dem sog. stellaren Kontinuum,
entsprechend der Linie bei "1"), so zeigt sich, daß diejenige Kontinuumsstrahlung herausabsorbiert
wird, die in demjenigen Frequenzbereich liegt, der durch den Dopplereffekt des auf den Beobachters
zu kommenden Windmaterials beeinflußt wird: Dies entspricht Frequenzverschiebungen von Null bis
v¥. (In der Skizze ist stattdessen die Geschwindigkeit vm
angegeben, die der maximalen Geschwindigkeit entspricht, bei der noch ausreichend absorbierende
Teilchen vorhanden sind, mit vm £ v¥.)
Absorptionsprozesse finden in Teil "A" des Windes vor der Sternscheibe statt und
resultieren in dem dargestellten Absorptionsprofil. Man beachte, daß dieses asymmetrisch bzgl. der
"Nullfrequenz" ist, da nur dasjenige Kontinuum absorbiert werden kann, welches auch auf
den Beobachter zu kommt.
- Links und rechts des resultierenden Absorptionstroges (d.h. bei Dopplerverschiebungen entsprechend
größer vm und kleiner Null) sieht der Beobachter die ungestörte stellare Kontinuumsstrahlung,
da es in diesem Frequenzbereich kein absorbierendes Material gibt.
- Aufgrund der endlichen Lebensdauer des angeregten Zustandes wird nach der Absorption ein neues
Photon reemittiert.
- Insgesamt würde ein Beobachter das durch eine Vielzahl solcher Prozesse resultierende Emissionsprofil
sehen, das hier, da es sich um zusätzliche Strahlung handelt, bei Null "anfängt".
- Im Gegensatz zum Absorptionsfall sieht der Beobachter nun allerdings Strahlung aus Windbereichen,
die sich sowohl auf den Beobachter zu bewegen als auch von ihm entfernen. Drei verschiedenen Regionen
tragen zur Emission bei:
- Der Bereich A' vor der Sternscheibe, d.h. derjenige Bereich, der auch absorbiert. Hier sieht
man die in Richtung des Beobachters reemittierte Strahlung. Man erinnere sich (siehe Abschnitt
2), daß die Emission (fast isotrop!) Photonen in alle Richtungen "lenken" kann, d.h.
ein gewisser Bruchteil wird immer in Richtung des Beobachters abgestrahlt, die dieser dann auch
sieht!
- Der Bereich B vor der Symmetrieachse, der nicht vor der Sternscheibe liegt, aber auf den
Beobachter zu kommt. Die benötigten angeregten Elektronen resultieren dabei aus der - für den
Beobachter nicht sichtbaren - Absorption eines stellaren Kontinuums, welches ursprünglich nicht
auf den Beobachter gerichtet war.
Bereich A' und B erzeugen den hochfrequenten (linken) Teil des Profiles.
- Der Bereich C hinter der Symmetrieachse, der nicht von der Sternscheibe abgedeckt wird. Hier
sieht man zum Beobachter hin emittierte Strahlung, die mit der Absorption von ursprünglich vom
Beobachter weg gerichteten Kontinuum verknüpft ist. Da sich auch das emittierende Windmaterial
vom Beobachter entfernt, ist die zugehörige Frequenzverschiebung negativ.
- Das insgesamt emittierte Profil ist asymmetrisch, da der emittierende Bereich mit positiven
Geschwindigkeiten (positiven Frequenzverschiebungen) größer als der analoge Bereich mit negativen
Geschwindigkeiten (und negativen Frequenzverschiebungen) ist. Die Abbildung zeigt deutlich, daß
der emittierende "Zylinder" A' vor der Sternscheibe kein analoges Gegenstück
dahinter hat, da der Stern selbst diesen Bereich abdeckt.
- Der Grund, warum das Emissionsprofil sein Maximum bei Null hat und bei Frequenzverschiebungen
+/-vm verschwindet, ist aufgrund der herrschenden Geometrie einfach zu verstehen.
Die emittierenden Flächen gleicher Geschwindigkeit sind äußerst verschieden! Die größte
dieser Flächen liegt bei einer Geschwindigkeit Null, d.h. fällt mit der hellen Linie zusammen,
so daß auch die Emission bei Frequenzverschiebung Null am größten ist. Je höher die Windgeschwindigkeit,
um so kleiner ist allerding die zugeordnete emittierende Fläche, die für Geschwindigkeiten größer
als der Endgeschwindigkeit schließlich Null wird. Damit ist das Emissionsprofil auf den Geschwindigkeitsbereich
±vm eingeschränkt.
- Durch die Überlagerung des asymetrischen Absorptions- und Emissionsprofiles entsteht letztendlich
die dargestellte typische P Cygni Form.
Nachzutragen bleibt, daß der Prozeß natürlich nur dann wie beschrieben abläuft, wenn es überall genügend
Ionen gibt, die absorbieren und emittieren können. Wenn es nur wenige solcher Ionen gibt, wird das
Profil schwächer, d.h. sowohl seine Einsenkung als auch seine Höhe über "1" geringer. Insbesondere
kann es dazu kommen, daß man nur noch Material sieht, welches langsamer als die Endgeschwindigkeit ist.
In diesem Fall wird das P Cygni Profil dann schmäler, als es dem Dopplereffekt bzgl. einer Geschwindigkeit
±v¥ entspräche.
Diese und andere Reaktionen der Profilform werden wir nun im nächsten Abschnitt betrachten.
4.2 Diagnostik von P Cygni Profilen
In diesem Kapitel wollen wir nun klären, was man tatsächlich aus den P Cygni Profilen über die Bedingungen
im Wind lernen kann. Aus dem im vorhergehenden Abschnitt dargestellten Bildungsmechanismus ergeben sich
dabei im wesentlichen drei Möglichkeiten:
- Bestimmung der Endgeschwindigkeit: Falls überall im Wind genügend absorbierende
Ionen vorhanden sind, läßt sich durch simples Vermessen der "blauen" Kante die Endgeschwindigkeit
bestimmen. Man muß (im Prinzip) nur die Frequenz des Einbruchs im Kontinuum auf der linken Seite
messen und die Verknüpfung zwischen Frequenzverschiebung und Geschwindigkeit kennen. Diese ist durch
die einfache Dopplerformel
gegeben, wobei
Dn = nm -
n = Frequenz der blauen Kante - Frequenz des absorbierten Photons
ist und sich die Frequenz des absorbierten Photons aus der Energiedifferenz des angeregten und des Ausgangszustandes
des Elektrons berechnen läßt. (Welche Näherung geht hier ein?) In diesem Praktikumsversuch werden
Sie mit der entsprechenden Meßtechnik (und ihrer Problematik) eingehend vertraut gemacht.
- Bestimmung der Ionendichten: Falls das beobachtete Profil über die gesamte Breite nicht
die Null-Linie erreicht (man spricht dann von nicht gesättigten Profilen), läßt sich aus einem
Vergleich zwischen theoretisch berechneten und beobachteten Profilen der Dichteverlauf der absorbierenden
und emittierenden Ionen bestimmen. Man muß dann "nur" im theoretischen Profil die Ionendichte
so lange variieren, bis dieses mit dem beobachteten Profil übereinstimmt. Auf diese Weise kann man
unter günstigen Umständen die Massenverlustrate oder die Elementhäufigkeit der beitragenden Ionen
bestimmen! Auch diese Methode wird im Versuch angewendet.
- Bestimung der Form des Geschwindigkeitsfeldes: Vor allem dann, wenn das beobachtete Profil
gesättigt ist, d.h. im Bereich der blauen Kante auf "Null" geht, läßt sich durch Variation
der Form des Geschwindigkeitsfeldes in den theoretischen Profilen und Abgleich (= "Fit")
mit der Beobachtung diese Form bestimmen. Unterschiedliche Geschwindigkeitsfelder (z.B. steil oder
flach) führen nämlich zu unterschiedlichen Flächen gleicher Geschwindigkeit (s.o.) und verändern
damit die Form des Emissionsanteils und dadurch die Gesamtform des P Cygni Profiles! Die dadurch
resultierenden Ergebnisse sind meistens leider in hohem Maße mehrdeutig (Warum?), und wir werden
im Praktikum noch eine andere, bessere Methodik der Geschwindigkeitsfeld-Diagnostik (®
Ha-Profile) kennenlernen.
4.3 Theoretische P Cygni Profile: Reaktion auf Ionendichte und
Form des Geschwindigkeitsfeldes
In den oberen Abbildungen zeigen wir nun theoretische P Cygni Profile, die die beiden letzten Punkte
verdeutlichen, d.h. die Reaktion des Profiles auf Ionendichte und Geschwindigkeitsfeld.
Die zweite und dritte Abbildung (b = 0.7, 1.0, bzgl. der Definition von b siehe Kapitel 5.2) zeigt Profile, die für ein Geschwindigkeitsfeld berechnet wurden,
wie es aus der Theorie strahlungsdruckgetriebener Winde (Kap. 5) vorhergesagt wird. Die erste
basiert auf einem steileren Geschwindigkeitsfeld, d.h. hohe Geschwindigkeiten werden näher am Stern erreicht,
und die vierte auf einem flacheren Geschwindigkeitsfeld, d.h. der Wind erreicht hohe Geschwindigkeiten
erst weiter weg vom Stern. (Was hat es mit dem Wert b = 0.5 auf sich?)
MERKE: je flacher das Geschwindigkeitsfeld, desto höher ist die Emission!
Zusätzlich ist in jeder Abbildung die Ionendichte variiert, und zwar so, daß es sehr viele
Ionen gibt und das Profil gesättigt erscheint (gepunktet und strichpunktiert), für eine mittlere
(gestrichelt) und für eine geringe (durchgezogen) Ionendichte. Der Unterschied in den einzelnen Dichten
ist jeweils ein Faktor 10.
In allen Abbildungen wurde angenommen, daß die Ionendichte proportional zur gesamten Winddichte variiert.
Falls man davon abgeht, findet man erheblich unterschiedlichere Formen (s.u.)
MERKE: Ab einer gewissen Ionendichte ergeben sich praktisch keine unterschiedlichen Profile
mehr, deshalb spricht man auch von Sättigung!
Dupletts: Überlagerung zweier Profile
Figure 12: Reaktion eines P Cygni Dupletts auf Variation von Linienstärke und Geschwindigkeitsfeld
Wenn man sich die beobachteten P Cygni Profile (Kap. 3) etwas genauer ansieht, stellt man fest,
daß diese, bis auf die Linie von N
3+ (dreifach ionisierter Stickstoff bei ca. 1720 Å),
aus zwei Komponenten bestehen. Dies liegt daran, daß bei den meisten UV P Cygni Linien
zwei energetisch
sehr nahe beieinander liegende Grundzustände (von denen aus absorbiert werden kann, bzw. auf
die die Elektronen zurückfallen) vorkommen. Dies bedeutet, daß diese Linien aus zwei sich überlagernden
P Cygni Komponenten bestehen, man spricht hier von
Dupletts. Diesem Faktum ist bei der Diagnostik
natürlich Rechnung zu tragen.
Bzgl. der Bestimmung der Endgeschwindigkeit gilt noch immer, daß diese von der blauen Kante des Gesamtprofiles
abgelesen werden kann. Man muß nur die Frequenzverschiebung bzgl. der hochfrequenten Komponente
berücksichtigen. Die Abhängigkeit von Form des Geschwindigkeitsfeldes und Ionendichte ist in der vorhergehenden
Abbildung ersichtlich, wobei hier zwei Komponenten angenommen wurden, die eine Trennung entsprechend
der halben Endgeschwindigkeit des Windes haben sollen. Wie man sieht, ändert sich am prinzipiellen Verhalten
gegenüber dem Fall einer einzelnen Linie nichts!
5 Theorie strahlungsdruckgetriebener Winde - Eine Einführung
Im folgenden wollen wir uns etwas näher mit der Linienbeschleunigung in den Winden heißer Sterne beschäftigen.
Insbesondere wollen wir zeigen, wie der beschleunigende Mechanismus dazu führt, daßstellare Winde bestimmten
Skalierungsrelationen für Mdot und v¥ folgen, und daßeine geschickte
Kombination dieser Relationen in Zusammenhang mit einem atomphysikalischen Faktum eine neue Möglichkeit
eröffnet, heiße Sterne als Entfernungsindikatoren zu nutzen. Offenkundig kann die hier vorgestellte Theorie
nur die einfachsten Aspekte der tatsächlichen Verhältnisse aufzeigen. Weiterführendes Material findet
sich im Literaturverzeichnis.
5.1 Die Linienstrahlungsbeschleunigung
Im weiteren gehen wir davon aus, daßder stellare Wind sphärisch-symmetrisch und stationär
ist.
5.1.1 Impulsübertrag in einer Linie
Betrachten wir zunächst den Impulsübertrag durch die Absorption und Reemission von stellaren Photonen
in einer spektralen Linie (Übergangsfrequenz im atomaren System ni), wobei wir die endliche Profilbreite der Linie vernachlässigen wollen.
Bei diesem Prozess wird, pro Photon, ein radialer Impuls von
| DPradial
= |
h
c
|
(nein
cosqein - naus
cosqaus) |
|
(1) |
vom absorbierten ("ein") und reemittierten ("aus") Photon auf das absorbierende/
reemittierende Ion übertragen, wobei q der Winkel zwischen Richtung des Photons
und radialem Einheitsvektor (parallel zum Geschwindigkeitsvektor) ist, dem das Ion folgt.
Aufgrund der gleichen Wahrscheinlichkeit, mit der nach innen bzw. nach außen reemittiert wird, ist der
Mittelwert
während
da die Photonen vor der Wechselwirkung hauptsächlich aus Richtung des Sternes kommen, d.h. parallel zum
Geschwindigkeitsvektor propagieren. Damit resultiert im Mittel
Betrachten wir nun die in Abb. 13 skizzierte Situation, die den Ausschnitt
einer sphärischen Kugelschale (Geschwindigkeitszuwachs dv auf einer Skala
dr) im Wind zeigt. (Photosphärische) Photonen der Beobachterfrequenz = Startfrequenz
nobs können immer dann von einem Ion
absorbiert werden, wenn ihre Frequenz im atomaren Bezugssystem gleich der Übergangsfrequenz ni ist, d.h. aufgrund des Dopplereffektes
Figure 13: Skizze eines blauen Überriesen, der seine eigene Windhülle bestrahlt. Ln ist die spektrale Leuchtkraft bei Frequenz n,
v ist die Windgeschwindigkeit am Radius r and r die dortige Dichte. Die
eingezeichete Schale hat eine Masse von dm = 4 pr2
rdr.
|
|
|
|
|
|
|
|
|
| (nobs+ dnobs)
- |
ni
c
|
(v + dv) |
|
|
(5) |
|
gilt. Mit anderen Worten: Eine mögliche Absorption/Reemission, im weiteren kurz "Streuung",
bei höheren Geschwindigkeiten erfordert Photonen, die auch bei höheren Frequenzen starten. Das dem Geschwindigkeitsintervall
dv entsprechende Frequenzintervall ergibt sich damit aus Gl. 5
als
Berechnen wir nun die Strahlungsbeschleunigung obiger Schale "durch" die betrachtete Linie
über die Definition jeglicher Beschleunigung, d.h.
so ergibt sich diese, wenn wir den Impulsübertrag durch eine einzelne Streuung mit der Anzahl der im
entsprechenden Frequenzintervall zur Verfügung stehenden stellaren Photonen multiplizieren, und zwar
pro Zeiteinheit und Masse der beschleunigten Schale. Die Anzahl der Photonen pro Zeiteinheit ist dabei
| Nn = |
D(En/hn)
Dt
|
= |
Ln
Dnobs
h nobs
|
|
|
(8) |
wobei Ln die stellare Leuchtkraft (= abgestrahlte Energie pro Zeiteinheit
und pro Frequenz) bei der Frequenz n ist. Mit nein = nobs
resultiert damit die (radiale) Beschleunigung der Massenschale durch eine Linie
| gradi= |
Nn
áDPradialñ
Dt Dm
|
= |
h nobs
c
|
|
Ln
Dnobs
h nobs
|
|
1
Dm
|
= |
Ln
ni
c2
|
|
dv
dr
|
|
1
4 pr2 r
|
. |
|
(9) |
Wir erhalten also das Ergebnis, daßdie Linenstrahlungsbeschleunigung der Schale vom Geschwindigkeitsgradienten
in der Schale abhängt! (uff, Grübel, Grübel, ???) Eine sehr merkwürdige und in der Physik wohl
einmalige Abhängigkeit!
Bisher haben wir stillschweigend vorausgesetzt, daßalle Photonen, die auf die fragliche Ionenspezies
in der Schale treffen, tatsächlich absorbiert werden. Dies mußnatürlich nicht immer so sein und trifft
de facto nur dann zu, wenn genügend viele Ionen vorhanden sind, die absorbieren können. Mit anderen Worten:
die Wechselwirkungswahrscheinlichkeit (WWW, nicht zu verwechseln mit dem web) wurde bisher mit "1"
angesetzt, was zur Folge hatte, daßdie Beschleunigung keinerlei Abhängigkeit von irgendwelchen atomaren
Eigenschaften aufwies, sondern nur von der Bestrahlung und der hydrodynamischen Struktur abhing. Berücksichtigt
man eine endliche WWW, so ergibt sich diese als
wobei t die optische Tiefe im betrachteten Übergang bei r, v, dv
etc. ist (siehe unten). Aus dieser Eigenschaft lassen sich zwei Arten von Linien herauskristallisieren.
Für Linien mit t >> 1 (d.h., sehr vielen Ionen, sog. optisch dicken
Linien) gilt WWW » 1, während optisch dünne Linien mit t
<< 1 eine WWW » t haben. Die Strahlungsbeschleunigung
einer optisch dünnen Linie ist also um den Faktor t kleiner, als sie es im
optisch dicken Fall wäre. Im weiteren werden wir deshalb die (minore) Näherung verwenden, daßalle Linien
mit t ³ 1 sich als optisch dick entsprechend Gl. 9 verhalten, während Linien mit t < 1 als optisch dünn
definiert werden und ihre Beschleunigung mit der aktuellen optischen Tiefe (die dann natürlich von Details
des Überganges abhängt) modifiziert wird. Man vergleiche den in Kap. 4 geschilderten, analogen Unterschied
zwischen gesättigten und nicht-gesättigten P Cygni Profilen.
5.1.2 Linienensemble
Nun absorbiert natürlich nicht nur eine Linie, sondern eine (sehr) große Zahl (etliche Millionen), wobei
einige Zehntausend für die Gesamtbeschleunigung gradtot
relevant sind. Um also diese zu berechnen, müssen wir über alle einzelnen Beiträge summieren, und erhalten
|
|
|
|
å
duenn
|
gradi + |
å
dick
|
gradi |
|
|
|
|
|
|
|
1
4 pr2 c2
|
|
æ
è |
|
å
duenn
|
Ln
ni |
dv
dr
|
|
ti
r
|
+ |
å
dick
|
Ln
ni |
dv
dr
|
|
1
r
|
|
ö
ø |
|
|
|
(11) |
|
Die optische Tiefe der Linien läßt sich nun (im Rahmen einer gewissen Näherung, der sog. "Sobolev-"
oder Überschallnäherung) als Funktion des Geschwindigkeitsgradienten, der Dichte und der sog. Linienstärke
ki angeben. (Eigentlich sollte ki dimensionslos sein, deshalb treten in realiter
noch zwei Normierungsgrößen auf - welche könnten das sein? Aus Gründen der Vereinfachung begnügen wir
uns aber mit folgender Definition.)
Die wichtigste Eigenschaft der Linienstärke ist es, daßsie alle atom- und plasmaphysikalischen Details
des betreffenden Überganges enthält, und für die meisten Linien praktisch konstant im Wind ist.
Aus obiger Definition ist sofort ersichtlich, daßder "Grenzwert" k11,
der optisch dünne von optisch dicken Linien separiert, nur von den (lokalen) Windeigenschaften abhängt.
| 1 = |
k11
r
dv / dr
|
® k11 = |
dv / dr
r
|
|
|
(13) |
Man beachte, daßalso k11 im Gegensatz zu ki im allgemeinen
über den Wind variieren wird. Unter Verwendung dieser Größe läßt sich die gesamte Strahlungsbeschleunigung
folgendermaßen schreiben:
| gradtot= |
1
4 pr2 c2
|
|
æ
è |
|
å
ki < k11
|
Ln niki + k11 |
å
ki ³ k11
|
Ln ni |
ö
ø |
|
|
(14) |
Auch aus dieser Gleichung ist der Sättigungseffekt sofort ersichtlich: optisch dicke Linien verhalten
sich alle gleich, während optisch dünne Linien entsprechend ihrer jeweiligen Linienstärke reagieren.
Figure 14: Logarithmische Darstellung der Linienstärkenverteilungsfunktion eines stellaren
Windmodelles mit Tef f =40000 K.
Gepunktet sind die Ergebnisse aus einem Modellatmosphärencode, gestrichelt ein Potenzgesetzfit entsprechend
Gl. 15.
Die gesamte bisherige Vorgehensweise nützt uns bisher nicht allzu viel, da wir immer noch die Linienstärken
der optisch dünnen Linien benötigen. Für das weitere Vorgehen kommt uns nun jedoch ein interessantes
Faktum zu Hilfe, das nicht unmittelbar einsichtig ist und hier nur angegeben wird: Betrachtet man ein
großes Ensemble von Linien, so genügen diese Linien bzgl. ihrer Stärke einer einfachen Statistik
(vgl. Abb. 14): Die Anzahl der Linien in einem Frequenzintervall n,
n+ dn mit Linienstärken
ki, ki + dki kann durch ein Potenzgesetz
beschrieben werden
| dN(n,
ki) = - No fn(n) kia-2 dn dki, 0 < a
< 1, |
|
(15) |
wobei die Frequenzverteilung unabhängig von der Linienstärkenverteilung ist! (Die bislang unterdrückten
Dimensionen werden in No mitberücksichtigt.) Ersetzt man nun in
Gl. 14 die Summen durch entsprechende Doppelintegrale und verwendet (15),
so findet man
|
|
|
|
1
4 pr2 c2
|
|
ì
í
î |
|
ó
õ |
inf
0
|
|
ó
õ |
k11
0
|
ki Ln
n dN +
k11 |
ó
õ |
inf
0
|
|
ó
õ |
inf
k11
|
Ln
n dN |
ü
ý
þ |
|
|
|
|
|
|
|
|
4 pr2 c2
|
|
ì
í
î |
|
1
a
|
k11a + |
1
1 - a
|
k11a |
ü
ý
þ |
|
|
|
(16) |
|
Die zweite Gleichung zeigt zwei Punkte auf: Sowohl die optisch dicke als auch die optisch dünne Linienbeschleunigung
skalieren mit der gleichen Potenz a, und das Verhältnis dieser Beschleunigungen
ist durch a/(1-a) gegeben, entspricht also bei
einem Wert von a » 2/3 (Vgl. Abb. 14)
einem Faktor 2!
Unser endergebnis für die Linienbeschleunigung läßt sich also folgendermaßen formulieren:
| gradtot= |
const
4 pr2
|
|
æ
è |
|
dv / dr
r
|
|
ö
ø |
a
|
, |
|
(17) |
und hängt, bis auf die Normierungskonstante und den Exponenten, nur noch von hydrodynamischen Größen
ab. (Die wahre Kunst der Windrechnungen ist es jedoch, gerade diese beiden Größen, in die die Besetzungszahlen
aller beitragenden Ionen eingehen, konsistent zu berechnen!)
5.2 Lösung der Bewegungsgleichung
Nachdem wir nun einen (relativ einfachen) Ausdruck für die Linienbeschleunigung gefunden haben, können
wir uns daran machen, die hydrodynamische Struktur des Windes zu untersuchen. Dabei gilt es, folgende
hydrodynamische Gleichungen (für stationäre, sphärisch-symmetrische Strömungen) zu berücksichtigen:
1. Die Kontinuitätsgl.: Mdot = 4 pr2 rv,
2. die Impulsgl.: v [(dv)/(dr)] = -
[ 1/(r)] [(dp)/(dr)]- ggrav(1-G) +
gradtot,
3. die Zustandsgl: p = ra2,
wobei p der Druck, a die isotherme Schallgeschwindigkeit, ggrav
die Schwerebeschleunigung des Sternes und G das Verhältnis von Thomsonsbeschleunigung
(Strahlungsbeschleunigung aufgrund der Streuung von Photonen an freien Elektronen, µ
r-2) und Schwerebeschleunigung ist. Man beachete: G
< 1 für stabile Sterne, G = O[0.5] für Überriesen.
Diese Gleichungen wollen wir nun für den Überschallbereich des Windes lösen. In diesem Bereich lassen
sich die Druckkräfte vernachlässigen (warum?), und wir finden unter Verwendung der Kontinuitätsgleichung
und (17) die Bewegungsgleichung des Windes im Überschallbereich:
| r2 v |
dv
dr
|
= -GM(1-G)
+ C¢ L |
×
M
|
-a
|
(r2 v |
dv
dr
|
)a |
|
(18) |
mit Masse des Sternes M, gesamter Leuchtkraft L = òLn
dn und Konstante C'. (Wie lautet C'?)
Obige Gleichung läßt sich unter Verwendung der Variablen z=r2 v dv
/ dr,z = const, (alle anderen Größen konstant) einfach lösen (z.B. graphisch),
und wir finden nur dann eine eindeutige Lösung für die Massenverlustrate, falls gilt:
|
×
M
|
µ L[ 1/(a)] |
æ
è |
M(1-G) |
ö
ø |
1-[ 1/(a)]
|
, |
|
(19) |
während wir aus der Konstanz von z durch einfache Integration das von der Massenverlustrate unabhängige
Geschwindigkeitsgesetz
|
|
|
|
|
|
|
|
|
|
æ
è |
|
a
1-a
|
|
ö
ø |
1/2
|
|
æ
è |
|
2GM(1-G)
R*
|
|
ö
ø |
1/2
|
|
|
|
(20) |
|
finden. R* ist der stellare Radius, und der zweite Faktor, der
die Endgeschwindigkeit des Windes bestimmt, ist nichts anderes als die (photosphärische) Fluchtgeschwindigkeit
vesc.
Wie gesagt, ist die gesamte obige Ableitung in einigen Teilen stark vereinfacht. Zieht man jedoch die
Analyse vollständig durch (die entsprechenden Verfeinerungen werden im Praktikum besprochen), so ergeben
sich keine gravierenden Änderungen. So bleibt die Skalierungsrelation für Mdot vollständig erhalten,
und auch an der Proportionalität v¥ µ
vesc ändert sich nichts. (Nur die Proportionalitätskonstante ist
verschieden). Die wichtigste Änderung betrifft die Form des Geschwindigkeitsfeldes. Der Exponent
1/2 ist nicht mehr länger gültig, sondern
| v(r) = v¥ |
æ
è |
1- |
R*
r
|
|
ö
ø |
b
|
, |
|
(21) |
wobei in den meisten Fällen b » 0.8. Dieser Exponent
b entspricht der in Kap. 4 eingeführten Größe.
5.3 Die Windimpuls-Leuchtkraft-Relation (WLR)
Obige Skalierungsrelationen machen nun die Existenz der sog. Windimpuls-Leuchtkraft-Relation (WLR), die
erstmals von Kudritzki et al. 1 rein empirisch
gefunden wurde, auch von einem theoretischen Aspekt her einsichtig. Die "beobachtete" WLR für
galaktische Überriesen (die Sie im Rahmen des Praktikums ableiten sollen), liest sich folgendermaßen:
|
×
M
|
v¥(R*/Rsun)1/2
µ L1.46. |
|
(22) |
Benutzen wir andererseits unsere theoretischen Skalierungen, so finden wir für die (bzgl. des stellaren
Radius modifizierte) Windimpulsrate
|
×
M
|
v¥(R*/Rsun)1/2
µ L[ 1/(a)] |
æ
è |
M(1-G) |
ö
ø |
[ 3/2]-[ 1/(a)]
|
, |
|
(23) |
was in Hinblick auf die Massenabhängigkeit auf den ersten Blick einen erheblichen Unterschied ausmacht.
Erinnern wir uns jedoch, daß a » 2/3, so sehen
wir, daßdiese Abhängigkeit fast vollständig verschwindet, in Übereinstimmung mit dem empirischen Resultat,
was einem a-Wert von 0.68 entspricht! Zusammenfassend läßt sich also festhalten,
daßdie WLR ein Resultat der Skalierungsrelationen für linienstrahlungsdruckgetriebene Winde und des Exponenten
der Linienstärkeverteilungsfunktion ist. So erlaubt also ein mikrophysikalisches Resultat letztendlich
die Vermessung von im wahrsten Sinne des Wortes astronomischen Größen.
Letztlich stellt sich noch die Frage, wie diese WLR tatsächlich genutzt werden soll. Derzeit sind Mitarbeiter
der Heißsterngruppe unseres Institutes u.a. damit beschäftigt, bei Objekten mit bekannter Entfernung
und in Abhängigkeit vom "Metallgehalt" der Winde (Warum diese Abhängigkeit?), entsprechende
empirische Relationen zu erstellen, u.zw. auf die gleiche Weise, wie es in diesem Versuch für galaktische
O-Überriesen gemacht werden soll. Hat man einmal solche Relationen und kennt den Metallgehalt des Sternes
(aus einer detaillierten Liniendiagnostik), so läßt sich seine Entfernung in folgender Weise bestimmen:
- Die Effektivtemperatur Tef f
des Sternes wird über photosphärischen Analysen abgeleitet.
- Die Endgeschwindigkeit des Windes wird aus P Cygni Profilen gemessen.
- Aus der Ha-Linie wird die Meßgröße Q = Mdot/(R*/Rsun)3/2 (vgl. Kap. 7.2) bestimmt.
Wenn die (für die entsprechende Metallizität) gültige WLR
| log( |
×
M
|
v¥(R*/Rsun)1/2)
= x log(L/Lsun) + b |
|
(24) |
lautet, ergibt sich daraus der stellare Radius mittels
| log(R*/Rsun)
= |
logQ + logv¥- 4x log(Tef f/
Tef f sun )
- b
2x -2
|
|
|
(25) |
Aus dem Radius folgt schließlich die Entfernung des Sternes. Fehlerabschätzungen ergeben dabei, daßder
Entfernungsmodul einer Galaxie bei Verwendung von ca. 20 Objekten auf ±0.1m angegeben werden kann. Damit ist diese neuartige Vorgehensweise mindestens
genauso gut wie herkömmliche Methoden (hauptsächlich: Periode-Leuchtkraft-Relation von Cepheiden) und
wird eine unabhängige Bestimmung von Entfernungen auf "mittleren" Skalen und damit eine
weitere Eichung der Hubble-Konstanten ermöglichen.
6 Analyse von UV P Cygni Profilen - Bestimmung von physikalischen
Parametern
Aus den im Praktikumsversuch gefitteten UV-Profilen ergeben sich, neben der Meßgrößen v¥,
auch Werte, die den Verlauf der Linienopazität und damit der entsprechenden Besetzungszahlen repräsentieren.
Insbesondere in Fällen, in denen das Profil nicht gesättigt ist, lassen sich daraus interessante Größen
ableiten und mit theoretischen Vorhersagen vergleichen. Die entsprechenden Variablen seien (wie im zu
verwendenden Fit-Programm) k und a genannt (nicht zu verwechseln mit den Größen
gleichen Namens aus Kap. 5), und wir werden im folgenden zeigen, wie diese Größen mit tatsächlichen
physikalischen Parametern des Windes zusammenhängen.
Parametrisiert man nämlich die Besetzungszahldichte nl(r) des unteren absorbierenden Niveaus
des Übergangs über die Dichte und die Elementhäufigkeiten, kann man aus dem Linienprofil Information
über das Produkt aus Massenverlustrate Mdot und Ionisationsgrad X(v) gewinnen.
Die in Gl. 12 eingeführte optische Tiefe der betrachteten Linie läßt sich auch
folgendermaßen schreiben, wenn wir von nun an Geschwindigkeiten in Einheiten der Endgeschwindigkeit und
Radien in Einheiten des stellaren Radius messen
| t(v) = |
-
c
|
i
|
(v) llu
|
R*
v¥
|
|
1
dv / dr
|
: = |
dv / dr
|
|
|
(26) |
| mit |
k
|
: = |
pe2
mec
|
|
lluR*
v¥
|
flu nl(v). |
|
(27) |
[`(c)]i ist
die frequenzintegrierte Linienopazität und llu die Wellenlänge
des betrachteten Überganges. In der Definition von [`(k)]
(27), einer Größe, die der adäquat skalierten Opazität entspricht, ist der erste
Faktor der klassische Absorptionsquerschnitt und flu die quantenmechanische Korrektur, die
sog. Oszillatorenstärke. Ferner haben wir den im UV geringfügigen (negativen) Beitrag der stimulierten
Emission vernachlässigt.
Die Besetzungszahldichte nljk des Levels l in der Ionisationsstufe j von Element k kann über
den Anregungsgrad E, den Ionisationsgrad X und die relative Häufigkeit Ak
des Elements bezüglich Wasserstoff ausgedrückt werden:
| nljk = |
nljk
njk
|
|
njk
nk
|
|
nk
nH
|
nH |
|
(28) |
|
nljk
njk
|
= E(v) , |
njk
nk
|
= X(v) , |
nk
nH
|
= Ak |
|
Bezüglich der Umrechnung von Massendichten in Teilchenzahldichten kann man in guter Näherung für OB-Sterne,
die nicht zu weit entwickelt sind, annehmen, daß fast alle Materie aus Wasserstoff und Helium besteht:
| nH = |
r(v)
mH(1+4YHe)
|
, YHe
=nHe/nH |
|
(29) |
YHe ist die relative Häufigkeit von Helium zu Wasserstoff, mH ist die Masse des H-Atoms. Die Dichte r(v) erhält
man aus der schon eingeführten Kontinuitätsgleichung:
Einsetzen ergibt:
| nljk = E(v)X(v) |
4p R*2 v¥ mH(1+4YHe)
|
|
1
r2 v
|
|
|
(30) |
Aus einem Vergleich von (27) und (30) ist sofort ersichtlich,
daßdie skalierte Opazität im wesentlichen (d.h. bei konstantem Ionisationsgrad) mit 1/(r2
v) variiert. Deshalb führen wir als Fitgröße den schon oben erwähnten Parameter k(v) ein, der unserer
Linienstärke ki (vgl. Gl. 12) proportional ist:
|
k
|
(v) : = k(v) |
1
r2 v
|
Þ t(v) = |
k(v)
r2 v dv / dr
|
|
|
(31) |
also
| k(v) = E(v)X(v) |
R*v¥2
|
|
(pe2)/(mec)
4pmH
|
|
Ak
1+4YHe
|
flu llu |
|
(32) |
Bis auf E(v) und X(v) treten jetzt nur noch Konstanten auf, k(v) parametrisiert also direkt das Verhältnis
von Besetzungszahldichte nljk zur Dichte r(v). Im weiteren können
wir E(v) = 1 setzen, da wir uns in diesem Praktikum nur mit den sog. Resonanzlinien von N v und C iv
beschäftigen werden, die beide vom Grundzustand ausgehen und deren Besetzungszahl demzufolge in etwa
derjenigen der gesamten Ionisationsstufe entspricht. Unter dieser Bedingung ist k(v) direkt proportional
dem Ionisationsverlauf X(v):
|
×
M
|
X(v) = |
4pmH ( 1+4YHe )
|
R*v¥2 k(v) |
|
(33) |
Aus einer "Messung" von k(v) läßt sich also unmittelbar das Produkt von Massenverlustrate
und Ionisationsgrad bestimmen. Allerdings wird hier auch ein zentrales Problem bei der Analyse von
P-Cygni-Profilen im UV deutlich sichtbar. Die Bestimmung der Massenverlustrate allein aus den Resonanzlinien
wird ganz außerordentlich erschwert durch die nur sehr ungenaue Kenntnis des Ionisationsgrades X(v).
Alle anderen Größen (R*,v¥,Ak,YHe) sind meistens in vergleichsweise
guter Genauigkeit beschaffbar. Der Wert für X ist jedoch nicht mit einer empirischen Analysemethode ausschließlich
unter Verwendung der UV-Spektren bestimmbar. Dies erfordert entweder ein numerisches Atmosphärenmodell
oder er kann nur ermittelt werden, wenn die Massenverlustrate bereits anderweitig bestimmt worden ist
(z.B aus der Ha-Linie im Optischen, vgl. Kap. 7).
Eine häufig verwendete Größe, die direkt aus den Linienfits ableitbar ist, ist die Säulendichte Ncol der Absorber (in cm-2) zwischen
zwei Positionen im Wind:
|
|
|
| |
R2
ó
õ
R1
|
nl(R) dR
= R* |
v2
ó
õ
v1
|
nl(v) |
æ
è |
|
dv
dr
|
|
ö
ø |
-1
|
dv |
|
|
|
|
|
|
| |
mec
pe2
|
|
v¥
flullu
|
|
v2
ó
õ
v1
|
|
k(v)
r2 v dv / dr
|
dv
= |
mec
pe2
|
|
v¥
flullu
|
|
v2
ó
õ
v1
|
t(v)
dv |
|
|
(34) |
|
Im weiteren wollen wir nun unserer generalisiertes b-Geschwindigkeitsfeld
(Gl. 21) als Standard verwenden, wobei wir gegenüber der ursprünglichen
Definition eine Änderung durchführen (abgesehen von der Verwendung der skalierten Größen r, v):
| v(r) = |
æ
è |
1- |
b
r
|
|
ö
ø |
b
|
, b = 1 - vmin1/b |
|
(35) |
Durch die Einführung des Parameters b tragen wir dem Umstand Rechnung, daßder Wind schon zu Beginn eine
Anfangsgeschwindigkeit vmin haben soll, die in der Größenordung
der Schallgeschwindigkeit ( » .01v¥)
liegt. Mit dieser Vorgehensweise wird berücksichtigt, daßunterhalb des Schallpunktes die Druckterme dominieren,
so daßdas b-Feld dort nicht mehr gültig ist. (Wie sollte das Geschwindigkeitsfeld
unterhalb des Schallpunktes aussehen?) Des weiteren approximieren wir den Ionisationsverlauf durch ein
Potenzgesetz bzgl. der Geschwindigkeit (dies ist nur die einfachste Möglichkeit, es existieren weitaus
geschicktere Methoden), d.h.
wobei a der oben erwähnten Größe im Fitprogramm entspricht. Aufgrund max(v)
= 1 ist sofort zu ersehen, daßko dem Ionisationsgrad im Außenbereich des Windes entspricht,
und daßa > 0 ( < 0) einen nach innen abfallenden (bzw. ansteigenden)
Ionisationsgrad andeutet. a = 0 bedeutet natürlich konstante Ionisation.
Mit diesen Definitionen (35,36) und den aus dem Fitprogramm
bestimmten Größen b, ko und a läßt sich
die Säulendichte (34) abschätzen:
| Ncol(v1,v2)
= |
mec
pe2
|
|
v¥
flullu
|
|
ko
bb
|
|
v2
ó
õ
v1
|
v1/b-2+a dv |
|
(37) |
Bei Angabe dieser Größe geht die Information über den Verlauf der Ionisation natürlich verloren.
Definiert man jetzt einen ,,mittleren Ionisationsgrad'' [`X] als das Verhältnis
der Anzahl aller Ionen eines Elements in der Säule zur Gesamtzahl der Teilchen des Elements, dann erhält
man:
|
|
|
|
|
|
|
|
|
| |
4pmH (1+4YHe)
|
bb
R*v¥ Ncol(v1,v2) |
æ
è |
|
v2
ó
õ
v1
|
v1/b-2
dv |
ö
ø |
-1
|
|
|
|
(38) |
|
Man beachte, daßdie Angabe eines mittleren Ionisationsbruchteiles wiederum die Kenntnis von Mdot voraussetzt.
Die hier bereitgestellten Gleichungen sollen im Versuch dazu benützt werden, alle relevanten Größen abzuleiten.
7 Analyse des Ha-Profiles
In diesem letzten Kapitel der theoretischen Einführung wollen wir uns nun mit der Frage beschäftigen,
wie man die Massenverlustrate von stellaren Winden messen kann. Wie sich in den letzten Jahren herausstellte,
eignet sich dabei die Ha-Linie2
in vielerlei Hinsicht als besonders guter Indikator.
7.1 Warum Ha?
Das Zusammentreffen dreier günstiger Umstände ist dafür die Ursache:
- Die Ha-Linie ist eine sogenannte r2-Linie.
Im Gegensatz zu Resonanzlinien (insbesondere den im vorhergehenden Kapitel diskutierten UV-Linien
mit P Cygni Charakter), deren Opazität sich proportional zur Dichte verhält, gilt unter Windbedingungen
für eine Reihe von Linien zwischen angeregten Niveaus
| nl,j(l \not = 1) ~
ne nj+1 f(Te, ¼) |
|
(39) |
(nl,j : Besetzungszahlendichte von Niveau l in Ionisationsstufe j, Te
: Elektronentemperatur, ne : Elektronendichte). Die Besetzung
der verschiedenen angeregten Niveaus ist demnach immer proportional zum Produkt aus der Gesamtbesetzung
der nächsthöheren Ionisationsstufe und der Elektronendichte.
Aus dieser Tatsache folgt u.a., daßdas Verhältnis von Emissions- und Absorptionskoeffizient, die sog.
Linienquellfunktion SL (die im wesentlichen vom Verhältnis
der Besetzungszahlen des oberen und unteren Niveaus des Linienüberganges bestimmt wird), für Linienübergänge
oberhalb des Grundzustandes relativ konstant bleibt, solange dies auch für die Elektronentemperatur
Te(r) gilt. In guter Näherung entspricht die Linienquellfunktion
dann der Planckfunktion Bn(Te).
Verständlich wird dieses Verhalten dadurch, daßdie Population dieser angeregten Niveaus hauptsächlich
durch die Strahlungsrekombination (Elektron + Ion(j+1) + Photon ® angeregtes
Ion(j), gefolgt von einer Abregungskaskade nach unten) gefüttert wird, die aufgrund der (Maxwellschen)
Geschwindigkeitsverteilung von Elektronen und Ionen ein thermischer Prozess ist.
Für die im vorhergehenden Kapitel angesprochenen Resonanzlinien gilt hingegen SLResonanz ~ 1/r2¼3.
Dies liegt im wesentlichen daran, daßdiese Linien nur eine (Quasi-)Streuung der Photonen bewirken,
d.h. sich die Anzahl der vorhandenen Photonen mit dem anwachsenden Windvolumen verdünnt.
Wie wir weiter unten sehen werden, ist es gerade diese Konstanz der Ha-Linienquellfunktion,
die den signifikanten Unterschied der Form des Ha-Linienprofiles
gegenüber einem P Cygni Profil bewirkt; man vergleiche die beiden Profile auf dem Titelbild dieser
Anleitung3.
Handelt es sich schließlich bei der Ionisationsstufe (j+1) um die Hauptionsationsstufe (wie es z.B. bei
heißen Sternen für H ii der Fall ist), gilt damit im wesentlichen
und aus nlj ~ r2 folgt damit auch, daßdie Opazität ein
analoges Verhalten [`(c)]i ~ r2 aufweist.
In Sternwinden treten solche sog. Rekombinationslinien bei zunehmender Winddichte in Emission auf, wobei
die Äquivalentbreite proportional zum Quadrat der Winddichte ist (genauer gesagt zu [(Mdot2)/(R*3v¥3)], vgl.
Gl. 41); sie sind daher bessere Mdot-Indikatoren als Resonanzlinien, zumindest
solange die Winddichte nicht zu gering ist!
- Ha ist eine der stärksten Linien.
Da man einen empfindlichen
Indikator für die Winddichte haben möchte, benötigt man eine starke Linie (hohe Oszillatorstärke),
die zudem in merklicher Besetzungsdichte vorhanden ist. Gesucht ist also eine Linie mit starkem Emissionsverhalten
im Wind. Die stärkste r2-Linie im Optischen ist in O-Sternen
typischerweise die He ii l4686-Linie, gefolgt von der Ha-Linie.
- Das Verhalten von Ha ist gut verstanden.
Im Gegensatz
zu den He ii-Linien ist das Verhalten der Balmer-Linien in O-Sternen gut verstanden und kann durch
numerische Simulationen fast perfekt (gegenüber der Beobachtung) repräsentiert werden. Die Besetzungszahlstruktur
ist hier sehr stabil und relativ unempfindlich gegen Variation stellarer Parameter.
7.2 Ha-Profil und Massenverlustrate
Im folgenden wird der Zusammenhang zwischen Ha-Profil und Massenverlustrate
dargestellt. Wir verwenden dazu die gleiche (Sobolev-)Näherung wie auch schon in früheren Kapiteln, um
die optische Tiefe des Linienüberganges zu berechnen.
Ebenso vernachlässigen wir bei der Abschätzung des Produktes nenHII den geringen Metallgehalt (s.o., obwohl die Metallinien den Wind beschleunigen)
und berücksichtigen nur die Elemente H und He. Schließlich sind diese beiden Elemente bei O-Sternen fast
vollständig ionisiert:
| ne nH= |
1+YHeIHe
(1+4YHe)2
|
|
r2
mH2
|
|
|
(41) |
(IHe : Anzahl freier Elektronen pro Heliumatom = 2 unter den geschilderten
Bedingungen). Analog zu Gl. 26 lautet die optische Tiefe
| t = |
-
c
|
i
|
(r) l23
|
R*
v¥
|
|
1
dv / dr
|
= |
A(r)
r4v2 dv / dr
|
|
|
(42) |
Im Parameter A sind alle Konstanten des Linienübergangs und alle Windparameter enthalten. Der entscheidende
Unterschied zur optischen Tiefe von Resonanzlinien liegt darin, daßder Nenner nun aufgrund der r2-Abhängigkeit
von [`(c)]i
einen zusätzlichen Term r2 v enthält!
Unter Verwendung der Saha-Boltzmanngleichung, der Kontinuitätsgleichung, Gl. (41,
42) und der atomaren Konstanten des Überganges finden wir für die Größe A(r)
| A(r)=Fa ·Te-1.5 |
é
ë |
b2(r) exp |
æ
è |
3.945
Te
|
ö
ø |
-b3(r) exp |
æ
è |
1.753
Te
|
ö
ø |
ù
û |
|
1+IHeY
(1+4Y)2
|
|
R*3 v¥3
|
|
|
(43) |
(Mdot in 10-6 Msun/a, v¥
in 1000 km/s, R* in Sonnenradien Rsun und Te in 104 K). In den Vorfaktor F
gehen alle Konstanten, Umrechnungsfaktoren sowie Wellenlänge und Oszillatorenstärke des Übergangs ein.
Die (bei O-Sternen) geringfügigen Abweichungen der Besetzungszahlen von ihrem thermodynamischen Gleichgewichtswert
(Saha-Boltzmann) werden in Form der sogenannten Departurekoeffizienten berücksichtigt:
Die Departurekoeffizienten beschreiben demnach, bei einem aktuellen Wert von ne
nj+1, die aktuellen NLTE4-Besetzungszahlen
in Einheiten der thermodynamischen Besetzung eines Niveaus i, und werden in unserem Fitprogramm aus Näherungen
an Ergebnisse von Modellrechnungen übernommen. Aufgrund der Nähe zum lokalen thermodynamischen Gleichgewicht
(s.o., "LTE") für Niveau 2 und 3 haben diese Koeffizienten einen Wert, der nicht allzu verschieden
von "1" ist.
Gl. 43 zeigt den grundsätzlichen Unterschied der Skalierungsrelationen zwischen
Resonanz- und Rekombinationslinien sofort auf. Während die optische Tiefe von Resonanzlinien von der
Kombination Mdot/(R*v¥2)
abhängt (vgl. 32), finden wir hier aufgrund der zusätzlichen r-Abhängigkeit
eine Funktion von Mdot2/(R*3 v¥3)!
Bei bekannter Endgeschwindigkeit sollten sich also (synthetische) Ha-Profile
kaum verändern, solange die Größe Q = Mdot/R*3/2 unverändert
bleibt. Dies ist der Grund, warum wir in Kap. 5.3 diese Kombination als eigentliche Meßgröße angeführt
haben.
Der Windparameter A bewegt sich für OB-Sterne typischerweise im Wertebereich zwischen 10-7
und 10-1, so daß die Ha-Linie
im größten Teil des Windes optisch dünn ist (vgl. (42)). Man kann davon ausgehen,
daß auch das Kontinuum in diesem Bereich optisch dünn ist. Bei der Berechnung des Profiles kann daher
in guter Näherung der Beitrag des Kontinuums zur Quellfunktion vernachlässigt werden; berücksichtigt
wird nur die Linienquellfunktion SL(r). Letztendlich ergibt sich
das Ha-Profil (in Einheiten des Kontinuums) in Sobolev-Näherung
wie folgt:
| Rx(x > 0)= |
|
1
2
|
|
ó
õ |
1
0
|
Px e-ts p
dp+ |
1
2
|
|
ó
õ |
¥
0
|
|
SL
Ic
|
( 1-e-ts ) p dp |
|
|
|
(45) |
| Rx(x < 0)= |
|
1
2
|
|
ó
õ |
1
0
|
Px p dp+ |
1
2
|
|
ó
õ |
¥
1
|
|
SL
Ic
|
( 1-e-ts ) p dp |
|
|
|
(46) |
(x=(n/n0-1)c/v¥, Px : photosphärisches Profil, Ic=Bn(Trad) Kontinuumsintensität bei x=0
(Linienmitte)). Das Kontinuum Ic wird durch die Planckfunktion
Bn berechnet, wobei Trad
die entsprechende photosphärische Strahlungstemperatur ist.
Figure 15: Schematische Darstellung der verschiedenen Windbereiche. In den Zonen rechts
und links neben der Sternscheibe ("core") sieht der Beobachter sowohl auf ihn zukommende
als auch sich von ihm wegbewegende Materie. Der dunkle Bereich ist für den Beobachter nicht sichtbar
und ist für die leichte Asymmetrie des beobachteten Profiles verantwortlich (zumindest solange nicht
perfektes LTE gilt). Der sog. Stoßparameter p variiert in dieser Skizze entlang der horizontalen
Achse. In der Sternmitte hat er den Wert "0", am rechten Rand der Sternscheibe den Wert
"1" und wächst nach rechts weiter an.
Die Interpretation dieser Gleichungen im Zusammenspiel mit Abb. 15 ist analog
zu der in Abb. 11 skizzierten Entstehung eines P Cygni Profiles. Der wesentliche
Unterschied ist hier der stärkere Abfall von t(v) nach außen, im Gegensatz
zur Quellfunktion, die praktisch konstant bleibt. Der blaue Teil des Profiles Rx(x > 0)
wird wiederum durch dasjenige Material verursacht, das auf den Beobachter zukommt bzw. durch Photonen,
die vom Stern abgestrahlt werden. Vor der Sternscheibe sieht man das photosphärische Ha-Profil Px, das vom Wind geschwächt wird. Die Emission stammt
vom zweiten Integral, dessen Beitrag umso größer ist, je größer die emittierende Fläche ist, d.h. maximal
bei x=0 ist und minimal dort, wo t praktisch verschwindet. Die größtmögliche
Breite des Profiles ist wiederum bei x=1 entsprechend v=v¥ gegeben.
Auf der roten Seite des Profiles Rx(x < 0) sieht man zum einen das ungeschwächte
photosphärische Profil, da bei diesen Frequenzen der Wind vor der Sternscheibe nicht absorbieren kann.
Man sieht hier nur den hinteren Wind, wobei sein Beitrag (2. Integral) symmetrisch zum blauen
Anteil ist.
Auf diese Weise wird die Variation des Ha-Profiles mit anwachsender
Massenverlustrate klar. Bei kleinem Mdot und entsprechend niedrigem t dominieren
jeweils die beiden ersten Integrale, exp(-t) ist klein und wir sehen ein symmetrisches
photosphärisches Profil. Wächst Mdot an, fangen die beiden zweiten Integrale an, merklich beizutragen,
und das photosphärische Profil wird langsam aufgefüllt, wobei das Resultat aufgrund der Asymmetrie des
ersten Anteils ein asymmetrisches Profil ergibt. Bei sehr hohen Massenverlustraten dominiert schließlich
der zweite Term vollständig, und wir erhalten ein praktisch symmetrisches Emissionsprofil, wie es auf
dem Titelbild dargestellt ist!
In diesem Fall ist, unabhängig von jeglicher Theorie des Strahlungstransportes, die Ha-Emission
einfach zu verstehen. Wir sehen im wesentlichen Photonen, die in einem sehr großen Volumen emittiert
werden, u.zw. aufgrund der Elektronenkaskade von Niveau 3 auf Niveau 2. Da es sich hierbei
um zusätzliche Photonen (verglichen mit dem rein stellaren Kontinuum) handelt, mußdas Profil in Emission
erscheinen. Um die Form des Profiles allerdings zu verstehen, sollte man sich auf jeden Fall den
Einflußdes Dopplereffekts vor Augen führen.
8 Durchführung des Versuches
Alle notwendigen Daten und Parameter finden Sie im Anhang!
8.1 UV-Analyse
Analysieren Sie die N v und C iv Linie für die im Anhang aufgeführte Stichprobe galaktischer O-Sterne.
Die notwendigen Programme, Daten und zu erzeugenden Output-Dateien befinden sich im Katalog "uv".
Die für die Linienfits benötigten IDL-Routinen (keine Angst, alles ist so programmiert, daßSie nicht
die geringste Ahnung bzgl. dieses Graphikpaketes haben müssen) lauten uv.pro und plotuv.pro, der output
wird in den Unterkatalog "catout" geschrieben.
8.1.1 Parameterstudie
Um ein "Gespür" dafür zu bekommen, wie die Profile auf die Variation der verschiedenen Parameter
reagieren, sollen in einer ersten Testreihe bei drei festgehaltenen Parametern jeweils der vierte
variiert werden. Schauen Sie sich die entsprechenden Reaktionen gut an, versuchen Sie sie zu verstehen
und in den späteren Fits anzuwenden. Führen Sie dazu insgesamt folgende Tests durch. Als Grundparameter
verwenden Sie
- v¥= 2000 km/s
- b = 1
- log ko = 0
- a = 0
Um das Simulationsprogramm zu starten, geben Sie in "IDL" den Befehl
uv,'testname','000',nvprof,civprof
ein. Für testname suchen Sie sich einen jeweils schlüssigen Namen aus, mit dem Sie auch
später die Ergebnisse identifizieren können. (Die Anführungszeichen müssen Sie mit eingeben). Die
Identifikation `000' besagt hier, daßmit keiner Beobachtung verglichen werden soll.
Das weitere Vorgehen ist fast selbsterklärend, Fragen werden beim Versuch beantwortet. Folgende Testreihen
sind durchzuführen:
- Test1: v¥ = 500, 2000, 4000 km/s
- Test2: b = 0.5, 0.8, 1., 2.
- Test3: log ko = -2, -1,
0, 1
- Test4: a = 2., 0., -3.
Nachdem Sie mit einer Testreihe fertig sind, geben Sie nach Aufforderung "HARDCOPY?"
die Antwort "0" (nein) ein. Die Druckaufbereitung erfolgt hier in einer separaten Prozedur
"plotuv":
plotuv,'testname',nvprof
und
plotuv,'testname',civprof
(in den Vektoren nvprof, civprof sind die Ergebnisse aus "uv" zwischengespeichert.)
Wiederum ist das weitere Vorgehen selbsterklärend. Falls Sie mit dem Bild zufrieden sind, geben Sie
nach Abfrage die Option "HARDCOPY = 1" ein. Es werden dann druckbare ps-files im Katalog
catout erzeugt, mit dem Namen testnameNV_uv.ps bzw testnameCIV_uv.ps.
Nochmals: Überlegen Sie sich sinnvolle und verschiedene Bezeichnungen für testname.
Vergessen Sie zum Schlußdes Praktikums nicht, alle output-Dateien auch tatsächlich auszudrucken.
8.1.2 Analyse der galaktischen Stichprobe
Bestimmen Sie nun aus der N v und C iv Linie Endgeschwindigkeit v¥
und, soweit möglich, b, ko,a für
die im Anhang aufgeführten O-Sterne (bis auf die Sterne HD 93128, HD 18409, HD 193514
und a Cam, für die wir keine aufbereiteten Beobachtungen haben. Die in der
Tabelle angegebenen Endgeschwindigkeiten dieser Sterne, die wir für die Ha-Analyse
benötigen, wurden entweder über den Spektraltyp geschätzt (HD 93128, HD 18409) oder aus unabhängigen
UV-Untersuchungen gewonnen (HD 193514, a Cam).)
Falls Sie zu dem Schlußgelangen, daßb nicht abgeschätzt werden kann, verwenden
Sie b = 1.0 für Überriesen und b = 0.8 sonst. Bei
gesättigten Linien versuchen Sie zumindest, eine Untergrenze für ko zu bestimmen.
Das zu verwendende Fitprogramm ist wiederum "uv", und wird hier folgendermaßen aufgerufen:
uv,'sternname','xxx'
wobei `sternname' der Name des Sterns und `xxx' (wiederum in Anführungszeichen) die file-Nummer
der entsprechenden Beobachtung ist (siehe Tabelle 1). Nachdem Sie einen zufriedenstellenden Fit erzeugt
haben, geben Sie nach Aufforderung "HARDCOPY?" nun den Wert "1" (ja) ein. Ein druckaufbereitetes
file mit den beiden Linien wird dann unter "catout/sternname_uv.ps" erzeugt. Vergessen Sie
nicht, die endgültig abgeleiteten Parameter zu protokollieren!
Tip: Bestimmen Sie als erstes v¥. Verwenden Sie
als Startwerte log ko = 1 und a = 0. Erst nachdem Sie v¥ für beide Profile bestimmt haben, sollten Sie mit einer Variation der anderen
Parameter beginnen. Beachten Sie allerdings: Bei nicht-gesättigten Profilen müssen v¥, ko
und a parallel gefittet werden!
Anmerkung: Einige Profile lassen sich auch bei größter Anstrengung im Bereich des blauen
Anstiegs zum Kontinuum nicht fitten. Versuchen Sie hier nur, Grenzwerte zu ermitteln und konzentrieren
Sie sich auf den Außenbereich des Windes. Die Ursache für die Problematik wird im Praktikum besprochen.
8.2 Ha-Analyse
Bestimmen Sie die Massenverlustraten und, soweit möglich, den Geschwindigkeitsexponenten b
für unsere Stichprobe. Arbeiten Sie jetzt im Katalog `halpha'. Die output-files (wiederum durch HARDCOPY
= 1 zu erzeugen) werden auch hier im Unterkatalog "catout" unter dem Filenamen `Sternname_ha.ps'
generiert. Das zu verwendende Fit-Programm lautet unter IDL "ha" und wird wie folgt aufgerufen
ha,'filename',vsini=x
bzw.
ha,'filename',vsini=x,vrad=y,
falls in der Tabelle ein expliziter Wert angegeben ist. Die Routine fragt Sie dann nach
den Sternparamteren und v¥ ab, bevor Sie einen Fit von Mdot
und b ermöglichen können. Spielen Sie beim ersten Fit mit diesen Parametern
etwas herum, um die Reaktion auf beide Fitgrößen kennenzulernen. Falls ein Fit von b
nicht möglich ist (wann ist das der Fall?), verwenden Sie die gleichen Standardwerte wie beim UV-Fit.
Nachdem Sie die Stichprobe analysiert haben, suchen Sie sich einen besonders "schönen"
Fall heraus. Zeigen Sie, daßdie eigentliche Meßgröße Q (vgl. Kap. 5.3) ist!
Vergessen Sie wiederum nicht, die abgeleiteten Werte zu protokollieren.
Anmerkung1: Auch bei diesen Profilen lassen sich einige auf der blauen Seite nicht
fitten. Konzentrieren Sie sich hier auf den roten Flügel. Die Ursache für die auftretenden Diskrepanzen
werden wiederum im Praktikum besprochen.
Anmerkung2: Der Grund, warum in der Ha-Analyse die
projizierte Rotationsgeschwindigkeit v sini berücksichtigt werden muß, bei der UV-Analyse hingegen nicht
(zumindest in einer ersten Näherung), wird ebenfalls während des Praktikums besprochen.
9 Ausarbeitung
9.1 Fragen zur Theorie
- Beantworten Sie die in Kap. 1 bis 7 eingestreuten 9 Fragen.
- Welche Annahme wurde stillschweigend bei der Ableitung der WLR gemacht? (Tip: Welche Abhängigkeit
von Mdot wurde in den Skalierungen vernachlässigt?)
- Skizzieren Sie die Flächen gleicher Geschwindigkeit für ein b = 1
Feld in Abhängigkeit der Beobachterfrequenz -1 £
x £ 1,Dx = 0.2 in der sog. p-z
Geometrie (Vgl. Abb. 15, p horizontal, z nach oben oder unten) auf. Berücksichtigen
Sie dabei, daß, bei Verwendung der skalierten Geschwindigkeit
| x = mv(r), m = cosq, m = z/r und z2+p2
= r2 |
|
(47) |
gilt. Überlegen Sie sich, was man aus diesen Flächen über die Form des P Cygni Profiles ableiten
kann.
9.2 Bestimmung von Säulendichten etc. und Ableitung der WLR für
galaktische Überriesen
- Diskutieren Sie die Ergebnisse Ihrer Parameterstudie der UV-Dupletts und versuchen Sie, die einzelnen
Reaktionen kurz zu begründen.
- Bestimmen Sie aus den Fitdaten der UV Profile und der Ha-Analyse
Werte (bzw. Grenzwerte) für die Säulendichte Ncol und den mittleren
Ionisationsgrad [`X]k von N v und C iv im Geschwindigkeitsbereich
[0.2; 1] (Daten siehe Anhang). Zeichnen Sie die Ergebnisse für [`X]k
als Funktion von Tef f bzw L/Lsun
(getrennt für N v und C iv). Diskutieren Sie mögliche Trends.
- Vergleichen Sie dort, wo es möglich ist, die Geschwindigkeitsexponenten aus der UV- und der Ha-Analyse.
- Zeichnen Sie die modifizierten Windimpulsraten log(Mdotv¥(R*/Rsun)1/2) als Funktion von
log(L/Lsun). Unterscheiden Sie dabei Überriesen von anderen Leuchtkraftklassen durch verschiedende
Symbole.
- Bestimmen Sie durch einen least-square fit die WLR für galaktische O-Überriesen. Wie liegen im
Vergleich zu dieser Relation die Sterne anderer Leuchtkraftklassen, und woran könnte der Unterschied
liegen?
- Verwenden Sie "Ihre" WLR zur Bestimmung des Radius des Überriesen Melnick 42 (siehe
Titelbild und Abb. 9) in der LMC. (Welche Näherung geht bei dieser Vorgehensweise
ein?)
Parameter von Mk42: Tef f
= 50500 K, v¥ = 3000 km/s, Q = 2.64·10-7
Msun/a (zur Erinnnerung: Q = Mdot/(R*/Rsun)3/2).
- Bestimmen Sie schließlich die Entfernung zur LMC aus diesem Radius und folgender Relation
| log(R*/Rsun)
= 2.33 - 0.2 MV -
0.5 log(Tef f/K) |
|
(48) |
Wie lautet der Entfernungsmodul, wenn die visuelle Helligkeit von Mk42 V = 12.64m
und die Verrötung AV = 1.24m ist? Bestimmen Sie
schließlich aus dem Modul die Entfernung in kpc!.
Fügen Sie Ihrem Praktikum die Abbildung aller erzielten Fits (incl. der "Q-Analyse") bei (in
vernünftiger Ordnung). Falls Sie für einzelne Objekte keine guten Fits erzielen konnten, begründen Sie
exemplarisch, weshalb Sie die von Ihnen gewonnene Lösung gegenüber anderen Möglichkeiten bevorzugen.
10 Schlußbemerkungen
In diesem Praktikumsversuch haben wir (hoffentlich) gezeigt, wie man die Spektren heißer Sterne nutzen
kann, um essentielle Informationen über deren Winde zu erlangen und eine neue Methode zur extragalaktischen
Entfernungsbestimmung zu entwickeln.
In realiter ist das gesamte Vorgehen natürlich um einiges komplexer, als es im Rahmen eines zweiwöchigen
Versuches herausgearbeitet werden kann. Die bisher an unserem Institut und an anderen Observatorien erzielten
Analysen haben letztendlich folgendes Bild ergeben:
- Die Theorie linienstrahlungsdruckgetriebener Winde ergibt eine sehr gute Übereinstimmung mit
der Beobachtung, d.h. die Linienbeschleunigung ist der dominierende Beschleunigungsmechanismus
der Winde heißer Sterne.
- Bezüglich vieler und teilweise wichtiger Details muß aber noch etliche Arbeit geleistet werden,
um auch diese zu verstehen.
- Beispiele hierfür sind u.a. der Einfluß der Rotation der Sterne auf ihre Winde (heiße
Sterne rotieren sehr schnell, bis zu einigen hundert km/s), und das Faktum, daß die Winde dieser
Sterne zeitlich veränderlich sind.
- Die Klärung dieser und anderer Fragen ist das Ziel gegenwärtiger Untersuchungen an der Sternwarte
München und an anderen Orten weltweit.
11 Anhang: Tabellen und notwendige Daten
11.1 Die Stichprobe galaktischer O-Sterne
Table 1: Parameter der zu analysierenden Stichprobe galaktischer O-Sterne.
Tef f in kK, R*
in Rsun, vrad, v sini, v¥
in km/s, Mdot in 10-6 Msun/a. "used" bezeichnet den effektiven Wert von v sini, falls dieser verschieden
vom photosphärischen Wert ist. Im Versuch ist dann dieser Wert zu verwenden. Die Werte für die Radialgeschwindigkeit
vrad - falls angegeben - beziehen sich auf arbiträre Verschiebungen
des beobachteten Profils und haben nichts mit den tatsächlichen Werten zu tun.
1)
Filename des beobachteten Ha-Profiles, zu verwenden in der Prozedur
"ha"
2) Filenummer des beobachteten UV-Profiles, zu verwenden in der Prozedur
"uv"
3) Fit-Wert aus Hg(photosphärisches
plus Windprofil).
4) "Wahrer" Wert incl. Korrekturterme für Windeffekte und
Zentrifugalkräfte.
5) v¥ geschätzt vom Spektraltyp
|
|
|
|
|
|
|
|
|
|
|
|
|
| star |
classif. |
file1) |
no.2) |
Tef f |
R* |
log g3) |
log g4) |
Y |
vrad |
v sini |
used |
v¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
| HD 93128 |
O3 V ((f)) |
HD93128 |
|
52.0 |
10. |
4.00 |
4.00 |
0.10 |
-10 |
100 |
|
31005) |
| HD 93250 |
O3 V ((f)) |
HD93250 |
088 |
50.5 |
18. |
3.95 |
4.00 |
0.10 |
|
100 |
|
|
| HD 93129A |
O3 I f* |
HD93129A |
079 |
50.5 |
20. |
3.80 |
3.95 |
0.10 |
|
130 |
|
|
| HD 303308 |
O3 V ((f)) |
HD303308 |
195 |
48.0 |
12. |
4.05 |
4.10 |
0.10 |
|
100 |
|
|
| z Pup |
O4 I (f) |
HD66811 |
061 |
42.0 |
19. |
3.50 |
3.60 |
0.12 |
|
220 |
|
|
| HD 15558 |
O5 III (f) |
HD15558 |
012 |
48.0 |
21.8 |
3.80 |
3.85 |
0.08 |
-75 |
120 |
|
|
| HD 15629 |
O5 V ((f)) |
HD15629 |
014 |
47.0 |
14.2 |
3.90 |
3.90 |
0.08 |
-75 |
90 |
|
|
| HD 14947 |
O5 I f+ |
HD14947 |
010 |
43.5 |
16.1 |
3.45 |
3.50 |
0.18 |
-25 |
140 |
|
|
| l Cep |
O6 I(n) fp |
HD210839 |
187 |
38.0 |
19. |
3.60 |
3.65 |
0.10 |
|
210 |
|
|
| HD 190864 |
O6.5 III (f) |
HD190864 |
171 |
41.0 |
14.1 |
3.55 |
3.55 |
0.20 |
|
105 |
|
|
| HD 217086 |
O7 V n |
HD217086 |
190 |
40.0 |
10.3 |
3.60 |
3.75 |
0.20 |
|
375 |
290 |
|
| HD 192639 |
O7 Ib (f) |
HD192639 |
174 |
38.5 |
19.5 |
3.40 |
3.45 |
0.25 |
|
125 |
|
|
| HD 193514 |
O7 Ib (f) |
HD193514 |
177 |
38.0 |
19.8 |
3.40 |
3.45 |
0.14 |
|
105 |
|
2200 |
| HD 203064 |
O7.5 III:n ((f)) |
HD203064 |
181 |
37.5 |
14.1 |
3.50 |
3.65 |
0.14 |
|
315 |
190 |
|
| x Per |
O7.5 III (n)((f)) |
HD24912 |
019 |
36.0 |
25.5 |
3.30 |
3.40 |
0.22 |
55 |
250 |
100 |
|
| HD 13268 |
ON8 V |
HD13268 |
006 |
35.0 |
11.7 |
3.30 |
3.50 |
0.25 |
-120 |
320 |
250 |
|
| HD 191423 |
O9 III:n* |
HD191423 |
173 |
34.0 |
13. |
3.40 |
3.70 |
0.25 |
-70 |
450 |
300 |
|
| HD 207198 |
O9 Ib-II |
HD207198 |
183 |
34.0 |
15.1 |
3.30 |
3.30 |
0.14 |
|
80 |
|
|
| HD 210809 |
O9 Iab |
HD210809 |
186 |
33.0 |
21.7 |
3.10 |
3.15 |
0.14 |
|
100 |
|
|
| z Oph |
O9 III |
HD149757 |
124 |
32.5 |
12.9 |
3.70 |
3.85 |
0.19 |
|
400 |
300 |
|
| HD 209975 |
O9.5 Ib |
HD209975 |
185 |
32.5 |
17.2 |
3.20 |
3.20 |
0.10 |
-30 |
100 |
|
|
| HD 18409 |
O9.7 Ib |
HD18409 |
|
31.5 |
16.1 |
3.10 |
3.15 |
0.14 |
-55 |
160 |
80 |
17505) |
| a Cam |
O9.5 Ia |
HD30614 |
029 |
30.0 |
29. |
2.95 |
3.00 |
0.20 |
|
80 |
|
1550 |
11.2 Einige benötigte Daten
Tef fsun
= 5780 K
Rsun = 6.96 ·1010 cm
ein Jahr
= 3.1558 ·107 s
pe2/(me c) = 0.02654 in cgs
mH = 1.673 ·10-24
g
Daten für die N v Linie (blaue Komponente, solare Häufigkeit)
flu = 0.157
llu
= 1238.8 Å
logAN = -4.01
Daten für die C iv Linie (blaue Komponente, solare Häufigkeit)
flu = 0.1908
llu
= 1548.2 Å
logAC = -3.42
Fußnoten:
1Kudritzki, R.P., Lennon, D.J., Puls, J.,
1995, "Quantitative Spectroscopy of Luminous Blue Stars in Distant Galaxies". In: ESO Astrophysics
Symposia, Science with the VLT, eds. J.R. Walsh and I.J. Danziger, Springer, Heidelberg, p. 246
2Übergang zwischen Niveau 2 und 3 im Wasserstoffatom
3Tatsächlich ist dieser starke Unterschied
nur bei OB-Sternen zu verzeichnen. Die wesentlich kühleren A-Überriesen zeigen ein Ha-Profil,
daßeinen typischen P Cygni Charakter hat: dies liegt an der Unterschiedlichen Ionisations- und Anregungsstruktur
von Wasserstoff, die dazu führt, das sich das zweite Niveau praktisch wie ein Grundzustand verhält.
4non local thermodynamic
equilibrium