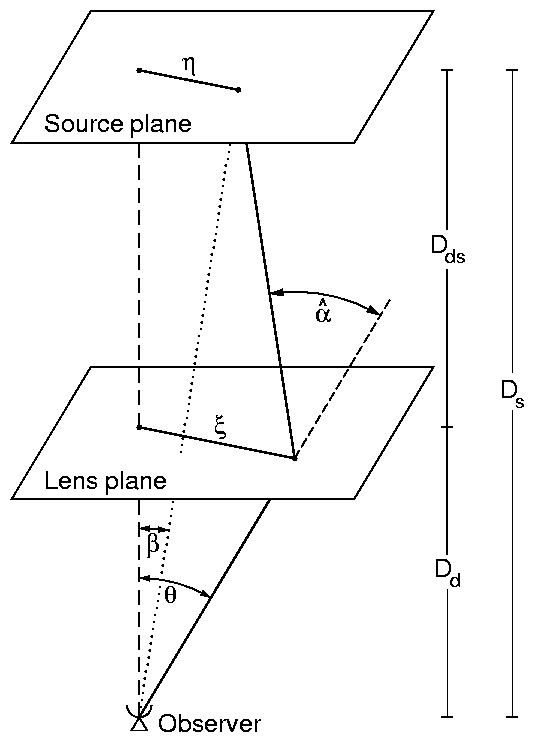
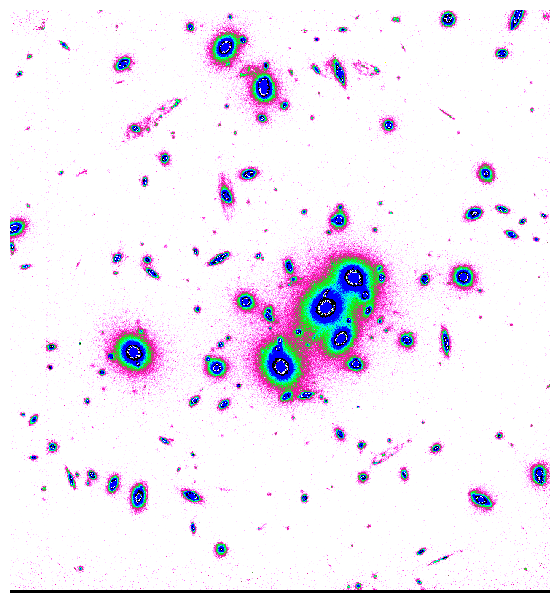
Fig..  Der Galaxienhaufen Cl0024+1654

1 Gravitative Lichtablenkung: vom Thema für Träumer zum kosmologischen Werkzeug

In ihrer ersten Phase, vor 1979, war die Theorie der Lichtablenkung in einem Gravitationsfeld zwar ausgearbeitet [siehe die Einleitung in Schneider, Ehlers & Falco, 1992, (SEF), Seite 1 bis 9] und experimentell durch die Messung der Lichtablenkung am Sonnenrand bestätigt, jedoch glaubten die meisten Astronomen, daß  dieser Effekt wegen seiner geringen Größ e (1¢¢.7 am Sonnenrand) für die Astronomie irrelevant ist. Arbeiten auf dem Gebiet der Gravitationslinsen wurden eher in die `Esoterik' als in die Astophysik eingeordnet: Sjur Refsdal (private Kommunikation) mußte aus seiner Dissertation 1963 das Kapitel über Gravitationslinsen streichen, um promoviert zu werden.

Der Wandel kam mit der Entdeckung des ersten doppelt abgebildeten Quasars durch D. Walsh, R.F. Carswell & R.F. Weymann (1979). Es ist kein Zufall, daß  die erste entdeckte mehrfach-abgebildete Quelle ein Quasar (quasai-stellare Radioquelle) ist: die Entdeckung von Linsenkandidaten und die Verifikation der Linsennatur ist einfacher, wenn die mehrfach-abgebildete Quelle ein Quasar bzw. ein QSO (quasi-stellares Objekt) ist:
i) Die punktförmigen Quasare sind sehr viel seltener als ausgedehnte Objekte (Galaxien), und selten findet man zwei von ihnen in einem Abstand von nur wenigen Bogensekunden. Beschränkt man sich auf helle QSOs (im optischen) und Quasare (im Radio-Frequenzbereich), findet man Linsenkandidaten auf eine effektive Weise.
ii) Ein Gravitationslinsenkandidat wird zu einem verifizierten System, wenn man zeigen kann, daß  die Bilder bis auf solche Abweichungen, die auf die Wirkung der Linse (Staub, Mikrolinseneffekt) zurückzuführen sind, identisch sind, wenn man eine potentielle Linse beobachten kann und wenn ein plausibles Linsenmodell die Bildkonfiguration erklärt. Da Quasare intrinsisch hell sind und ihre Spektren Strukturen, insbesondere starke Emissionslinien zeigen, kann man ihre Rotverschiebung und ihre spektralen Eigenschaften leichter und in kürzerer Zeit bestimmen, als dies für Galaxien gleicher Entfernung möglich ist.

Die zweite herausragende Entdeckung sind die groß en leuchtenden Bögen (`giant luminous arcs') von Soucail et al. (1987) und Lynds & Petrosian (1986): beide Gruppen beobachteten in der Sichtlinie zu Galaxienhaufen bogenförmige, lange und gleichzeitig dünne Quellen, deren Krümmungsradius mit dem Abstand vom Haufenzentrum oder der cD Galaxie eines Haufens übereinstimmt. Sie interpretierten diese Bögen als Galaxien hoher Rotverschiebung, die sich in der Nähe des Einsteinradius des Galaxienhaufens befinden und dort sehr stark verzerrt werden.

In beiden Fällen (den Mehrfachquasaren und Arcs) ging man nach der zufälligen Entdeckung einiger Arcs und Mehrfachlinsensystemen zu systematischen Himmelsdurchmusterungen (Surveys) über. Mit der systematischen Untersuchung der Linsenhäufigkeit und auftretenden Linsenkonfigurationen von vollständigen Quasar-Katalogen (diese Kataloge enthalten alle Quasare mit bestimmten Eigenschaften, die heller als ein bestimmtes Helligkeitslimit sind) und der Untersuchung von Arc-Konfigurationen in allen Galaxienhaufen heller als eine bestimmte Röntgenleuchtkraft begann man, den Linseneffekt als Werkzeug zu gebrauchen, um kosmologische und astrophysikalische Fragen zu beantworten.

1) Die Position und Form der Arcs und mehrfach abgebildete Galaxien schränken die Massenverteilung in den Zentren von Galaxienhaufen ein (Fort & Mellier, 1994).

2) Aus der Lichtlaufzeitdifferenz in einem Mehrfachlinsensystem kann man die Hubblekonstante H₀ bestimmen (Refsdal 1964, Kundic et al. 1996).

3) Man kann z.B. aus der Häufigkeit von mehrfach abgebildeten Quasaren und ihrer Bildaufspaltung die kosmologische Konstante L und den Zusammenhang zwischen Leuchtkraft und Geschwindigkeitsdispersion (L-s)-Relation einer Galaxie einschränken (siehe z.B. Kochanek, 1995).

Mehrfach abgebildete Quasare und Arcs haben drei Gemeinsamkeiten: sie sind spektakulär, relativ selten und aus ihnen entwickelten sich die beiden Hauptarbeitsrichtungen der momentanen Linsenbeobachtung und -forschung:

Von Mehrfachquasaren zum Microlensing und den Machos

Eine Galaxie besteht nicht nur aus glatt verteilter Materie (Gas und dunkle Materie), sondern auch aus kompakten Sternen. Diese führen zu einer Bildaufspaltung im Mikro-Bogensekundenbereich (Mikrolinseneffekt); die einzelnen Bilder sind zwar nicht auflösbar, jedoch verändern die Sterne die Gesamtverstärkung einer genügend kleine Quelle. Für kleine Quellen kommt es zu einer Zunahme der Wahrscheinlichkeit hoher Gesamtverstärkungsfaktoren, relativ zu dem Fall glatt verteilter Materie. (Der Erwartungswert der Verstärkung bleibt von der Granularität unberührt). Da i.a. Quelle, Linse und Beobachter relativ zu einander nicht ruhen, verändert sich die Verstärkung entlang der Sichtlinien zur Quelle mit der Zeit. Der Mikrolinseneffekt wurde als erstes in einem Mehrfachlinsensystem, dem sogenannten Einsteinkreuz [ein Quasar mit Rotverschiebung z = 1.69 wird von einer Galaxie bei z = 0.039 in vier Bilder abgebildet] nachgewiesen. Mit Hilfe der Variabilität der Quasar-Bilder im Einsteinkreuz wurde auch gezeigt, daß  die Quasare eine genügend kleine Ausdehnung haben, daß  diese Mikrolinsen-induzierte Variabilität auftritt. Nimmt man an, daß  die aus dem Einsteinkreuz abgeschätzte Quasar-Quellgröß e typisch ist, kann man umgekehrt aus der Variabilität der einfach abgebildeten Quasare eine obere Grenze für den Beitrag von kompakten Objekten in einem bestimmten Massenbereich zur Materiedichte des Universums angeben (z.B. Schneider 1993).

Sterne und andere kompakte Körper in unserer Galaxie üben auf Sterne entlang ihrer Sichtlinie (z.B. im galaktischen Zentrum oder in der Groß en Magellanschen Wolke) auch einen Mikrolinseneffekt aus. Zu jedem Zeitpunkt wird im Mittel einer von einer Million Sternen durch den Mikrolinseneffekt verstärkt. B. Paczy\' nski schlug 1986 vor, die Häufigkeit und Zeitdauer dieser Effekte zu beobachten, um mögliche Modelle über die Anzahldichte und Verteilung von kompakten Körpern (leuchtende Sterne, braune Zwerge, kleine schwarze Löcher, weiß e Zwerge...) in unser Galaxie einzuschränken. Diese Beobachtungen werden von mehreren Kollaborationen in Richtung der Magellanschen Wolken und des Zentrums unserer Galaxie mit viel Erfolg durchgeführt (Paczy\' nski, 1996). Sie werden uns u.a. zeigen, ob tatsächlich die `fehlende' Masse im Halo unserer Galaxie durch massive, kompakte Halo-Objekte (MACHOs) aufgebaut ist, wie im Zentrum die Sterne verteilt sind, und im Prinzip kann man mit dieser Methode sogar Planeten finden.

Von Arcs zu Arclets und parameterfreien Massenrekonstruktionen

Betrachtet man einen Galaxienhaufen, der Arcs zeigt, so sieht man auch kleinere Bögen, die `Arclets'. Sie sind wie die Arcs tangential zum Haufenzentrum orientiert und haben ein Länge- zu Breiteverhältnis, das von zufälligen Feldgalaxien überschreitet. Die `Arclets' sind wie die Arcs Galaxien, die durch das Gravitationspotential des Galaxienhaufens verzerrt abgebildet werden. Die Verzerrung ist zwar nicht so stark wie die der Arcs, dafür gibt es sehr viel mehr Arclets als Arcs (Arcs können sich nur entlang sogenannter kritischer Linien bilden, Arclets treten im gesamten Haufen auf, wenn die Lichtablenkung stark genug ist)! In Gebieten, in denen die Linsenwirkung des Haufens schwach ist (`weak lensing'), kann man `mit dem Auge' keine bevorzugte Ausrichtung der Galaxien mehr erkennen. Mit einer statistischen Analyse (z.B. Mittelung über die Elliptizitäten benachbarter Galaxienbilder) kann man jedoch zeigen, daß  im Mittel die Galaxien tangential zum Haufenzentrum ausgerichtet sind. In dem Fall einer schwachen Linse steht die mittlere Elliptizität der Galaxien in einem einfachen Zusammenhang mit der Massenverteilung des Haufens. Die Invertierung dieser Gleichung durch Kaiser & Squires (1993) liefert die Massenverteilung als Funktion der beobachteten Elliptizitäten und bereitete den Weg für nachfolgende Verbesserungen und Verallgemeinerungen.

Während der Mikrolinseneffekt Informationen über die Verteilung von kompakten Objekten in Galaxien (insbesondere unsere Galaxie) liefert, erhält man durch `weak lensing' Analysen die Massenverteilungen individueller Galaxienhaufen und Galaxiengruppen. Mit statistischen Mitteln kann man auch die Massenverteilung und Ausdehnung der Halos von Galaxien (durch `galaxy-galaxy lensing') und das Spektrum der Dichtefluktuationen im frühen Universum (durch Messung der `cosmic shear') einschränken.

Literatur

1) Das Buch `Gravitational Lenses' (SEF) von P. Schneider, J. Ehlers und E.E. Falco (Springer Verlag 1992) enthält fast alles, was Ihr schon immer über Gravitationslinsen wissen wolltet. Kapitel 1 faß t die Geschichte dieses Forschungsgebietes zusammen - auch für Laien geeignet (Bettlektüre?). In Kapitel zwei werden grundlegende Effekte des Linseneffekts erläutert und der Stand der Beobachtungen bis 1992 dargestellt. Das Handwerkszeug zur Untersuchung des Linseneffekts (Linsengleichung, Verstärkung, kritische Kurven etc.) wird in Kapitel 5 zur Verfügung gestellt.

2) Der Review `Arc(let)s in clusters of galaxies' (MB) von Y. Mellier und B. Fort (Astronomy & Astrophysics Review 1994) demonstriert u.a., wie man mit Hilfe von Arcs und Arclets in Galaxienhaufen die Massenverteilung in den Zentren von Galaxienhaufen einschränken kann. Die Theorie wird mit Beispielen in Figuren veranschanschaulicht. Die beiden Autoren - sie gehören zu den besten und erfolgreichsten Beobachtern auf diesem Gebiet - stellen die wichtigsten Beobachtungen, aber auch die daraus gewonnenen Informationen über die Massenverteilung in Galaxienhaufen bis zum Jahr 1994 zusammen.

3) Die `Lectures on Gravitational Lensing' (BN) (in der Anleitung begefügt) von M. Bartelmann und R. Narayan beschreiben u.a. das Prinzip des schwachen und starken Linseneffektes in Galaxienhaufen. Für dieses Praktikum reicht es, die Kapitel 2.1, 3.1,3.2.,3.4, 3.5, sowie 4.1 (am wichtigsten) verstanden zu haben. Ihr solltet auß erdem Kapitel 4.2 einmal durchlesen und das Prinzip wiedergeben können.

2 Grundlagen der Gravitationslinsentheorie

2.1 Das kosmologische Standardmodell

Im folgenden soll kurz das kosmologische Standardmodell beschrieben werden. Die nächsten zwei Seiten sollten für Euch (nach dem Besuch der Astronomie-Einführungsvorlesung) keine Neuigkeiten enthalten. Sie sollen die Erinnerung auffrischen und auch notwendige Notation einführen. Ausführliche Darstellungen über das Standardmodell können in Börner (1988), Peebles (1993), Weinberg (1972), Padmanabhan (1993) nachgelesen werden.

Man nimmt an, daß  die Raumzeit unseres Universums, wenn man es über genügend groß e Skalen, ³ 500 Mpc, (1pc » 3×10¹⁸ cm) gemittelt betrachtet, durch eine Robertson-Walker Metrik beschrieben werden kann:

L = 0 ist dies dann der Fall, wenn die heutige Materiedichte gleich der kritischen Materiedichte ist. Mit den oben eingeführten Bezeichnungen kann die Friedmanngleichung für die materiedominierte Phase des Universums unter Benutzung von

r = r_d+r_r » r_d µ R^-3 auch als

2.2 Kosmologische Rotverschiebung und Entfernungsmaß e

Rotverschiebung:
Beobachten wir zur Zeit t₀ Wellenfronten, die zur Zeit t_e von einer Quelle mit konstanten räumlichen Koordinaten, r, q, f = const, mit einer Frequenz n_e ausgesendet wurden, dann ist ihre Frequenz um einen Faktor 1+z verringert,

Winkelabstand:
Gegeben sei eine Quelle mit einer Ausdehnung der Eigenlänge dz und einer beobachteten Winkelausdehnung dq. Der Winkelabstand der Quelle beträgt dann in Anlehnung zur Euklidischen Entfernung: D = [(dz)/( dq)]. Für einen Beobachter und eine Quelle bei den Rotverschiebungen z₁ und z₂ folgt für flache Raumzeiten (k = 0) (vgl. Fukugita et al. 1992, Gleichung (16), Peebles 1993, Gleichung (13.30))

Leuchtkraftdistanz:
Für eine Quelle mit Fluß  s and Leuchtkraft L definiert man die Leuchtkraftdistanz als

Aufgaben:
· T1

· T2

· T3

· T4

2.3 Die Linsenabbildung

In diesem Abschnitt werden die wesentlichen Aspekte der Gravitationslinsentheorie beschrieben. Ausführlichere Darstellungen findet man in SEF, Kapitel 3 bis 5, in den Übersichtsartikeln von Blandford und Narayan (1992) und in meiner Diplomarbeit (Seitz 1993). R. Benders Vorlesungsskript enthält auch einen Abschnitt über Linsen. Dort könnt Ihr nachlesen, wie man den Ablenkwinkel (bis auf einen Faktor 2) erhält, wenn man die Lichtablenkung als Streung eines klassischen Teilchens mit Geschwindigkeit c an einem 1/r-Potential behandelt

2.3.1 Der Ablenkwinkel
Das Gravitationsfeld einer Massenverteilung lenkt Lichtstrahlen ab, die Richtungsänderung eines Lichtstrahls wird als Ablenkwinkel

Aufgabe:
· T5

2.3.2 Die Linsengleichung

Fig.2.1.  Geometrische Darstellung der Linsengleichung: Die gestrichelte Linie (wird als `optische Achse' bezeichnet), verbindet Beobachter, Linse und Quelle und legt den Koordinatenursprung in der Quell- und Linsenebene fest. Die gepunkteten und durchgezogenen Kurven geben an, wie der Lichtstrahl von der Quelle zum Beobachter in Abwesenheit und in Anwesenheit der Linse verläuft.

by Gegeben sei nun eine Quelle bei der Rotverschiebung z_s, ein Linse bei z_d und ein Beobachter bei z = 0; ferner seien D_s, D_d und D_ds die Winkeldistanzen vom Beobachter zur Quelle und Linse sowie von der Linse zur Quelle (siehe 2.8). Analog zur Linsenebene definieren wir eine Quellebene, deren Ursprung durch den Schnittpunkt der Quellebene mit der optischen Achse gegeben ist und die parallel zur Linsenebene ist. Sei x der Stoß vektor eines Lichtstrahls in der Linsenebene, sowie

Wie in der newtonschen Mechanik und in der klassischen Elektrodynamik stellt das Ablenkpotential y die grundlegende Größ e dar; der Ablenkwinkel kann damit als `Kraftfeld' interpretiert werden. Die Zusammenhänge von Ablenkpotential, Flächenmassendichte und Ablenkwinkel in der Linsentheorie sind analog derer von elektrischem Potential, Ladungsdichte und elektrischem Feld in der zweidimensionalen Elektrostatik.

2.3.3 Die Jacobimatrix der Linsengleichung
Betrachten wir nur Winkelbereiche, für die der Ablenkwinkel wenig variiert, so können wir die Linsengleichung linearisieren und erhalten die Jacobimatrix A der Linsenabbildung

Die Jacobimatrix beschreibt also, wie ein infinitesimales Lichtbündel von der Linsen- in die Quellebene abgebildet wird. Man verwendet sie, um (statistisch) die Veränderung der Form und Fläche von ausgedehnten Quellen auszuwerten, sowie, um die relative Form von ausgedehnten Mehrfachbildern zu untersuchen.

Die Jacobimatrix (2.16) zerfällt in einen Anteil (1-k)Á proportional zur Einheitsmatrix Á und einen spurfreien Beitrag, der durch die Scherung g beschrieben wird. Die Flächenmassendichte k führt zu einer isotropen Fokussierung eines Lichtbündels, die zwei-komponentige Größ e g bewirkt eine anisotrope Verzerrung . k und g entsprechen damit der Ricci- und Weylfokussierung von Lichtbündeln in der allgemeinen Relativitätstheorie (Seitz 1993, Seitz, Schneider & Ehlers 1994).

2.3.4 Kritische Kurven und Kaustiken
Die Jacobimatrix kann singulär werden (detA = 0). Dies ist der Fall, wenn [ 1-k(q) ]² - | g(q) |² = 0 ist, wobei ich g₁²+g₂² als | g|² abgekürzt habe. Die Punkte der Linsenebene, deren Jacobimatrix singulär ist, bilden geschlossene Kurven, die als kritische Kurven bezeichnet werden (SEF, Kapitel 5.2). Bildet man diese Kurven mit Hilfe der Linsengleichung (2.13) auf die Quellebene ab, erhält man die den kritischen Linien entsprechenden Kaustiken. Kaustiken separieren Gebiete in der Quellebene, in denen gelinste Quellen eine verschiedene Zahl von Bildern aufweisen. Überschreitet eine Quelle eine Kaustik, so entstehen, bzw. vergehen zwei Bilder an der zugehörigen kritischen Linie. Findet dieser Verschmelzungsprozeß  in radialer (tangentialer) Richtung zum Massenzentrum statt, so spricht man von radialen (tangentialen) kritischen Kurven und radialen (tangentialen) Kaustiken.

In den beiden Teilfiguren von Figur 2.1 sind jeweils links und rechts für eine elliptische Massenverteilung die kritischen Linien (also Bildebene) und Kaustiken (also Quellebene) dargestellt. Von auß en wird jeweils eine Quelle (rosa bzw. hellblau) in vier (drei) Schritten Richtung Massenzentrum (rote Quelle) geschoben. Die zugehörigen Bilder in der Linsenebene sind mit derselben Farbe in der linken Seite der Teilfigur eingezeichnet.

Linke Teilfigur: die hellblaue Quelle hat die äuß ere Kaustik überschritten, und es sind zwei zusätzliche Bilder in radialer Richtung an der inneren kritischen Linie entstanden. Es handelt sich also um eine radiale Kaustik, bzw. radial kritsche Linie. An der Position der dunkelblauen Quelle sind die zugehörigen Bilder von der radial kritischen Linie weggewandert (eins nach innen, wo es sehr klein und damit fluß abschwächend abgebildet wird, und eins nach auß en, wobei es seine Gestalt von radialer in tangentialer Verzerrung ändert). Hat die Quelle eine weitere Kaustik überschritten (grüne Quelle), so entstehen in tangentialer Richtung an der äuß eren kritischen Linie (also die tangential kritische Linie) zwei neue Bilder. Das fünfte Bild ist fast unmittelbar im Massenzentrum und so klein und schwach abgebildet, daß  es in der Figur schon nicht mehr zu sehen ist. Befindet sich die Quelle im Zentrum (rot), also auf der optischen Achse des Linsensystems, erhält man 4 fast kreisförmig angeordnete Bilder (und eines unsichtbares im Zentrum). Falls die Massenverteilung der Linse sphärisch symmetrisch ist, enstünde statt der vier roten Bildpositionen ein Kreis, der den Einsteinradius des Linsensystemes wiedergäbe.

In der rechten Teilfigur wird die Quelle nicht über ein gerades Stück (Falte) der tangentialen Kaustik geschoben, sondern über eine Spitze (Kuspe). Bei diesm Vorgang (blau zu grün) entstehen aus einem Bild drei Bilder. Man bezeichnet Bilder, die an einer Falte verschmelzen, als `fold-arc' und solche an einer Kuspe als `cusp-arc'. Cusp-arcs sind im allgemeinen größ er und stärker gekrümmt und damit auch spektakulärer als Fold-arcs.

Figure 2.1: Jede Teilfigur enthält rechts die Kaustiken (Quellebene) und links die zugehörigen kritischen Kurven (Linsenebene). Für 5 bzw. 4 verschiedene Quellpositionen sind die zugehörigen Bildpositionen in derselben Farbe eingezeichnet. Man kann die Bildung von radialen Arcs sowie Fold- und Cusp-Arcs an der tangentialen kritischen Linie mitverfolgen (mehr dazu im Text)

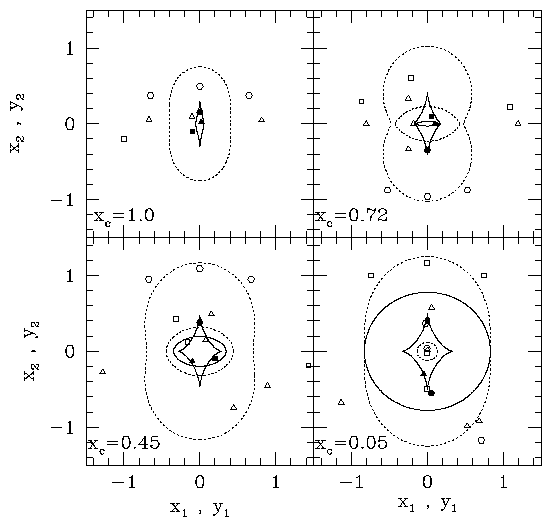
Fig.2.2.  Diese Figur soll verdeutlichen, welche Mehrfachbildkonfigurationen in Linsensystemen typischerweise auftreten. Dazu wurde ein eine isotherme Sphäre mit Kernradius x_c verwendet und eine zusätzliche äuß ere Scherung g = 0.2 angenommen. Der Kernradius wurde, wie in den 4 Teilfiguren eingezeichet, variert. Die Kaustiken bzw. kritischen Linien sind als durchgezogene Kurven und gestrichelte Kurven eingezeichnet. Die gefüllten Symbole repräsentieren jeweils eine Quellposition, die zugehörigen leeren Symbole die zur Quelle gehörende(n) Bildposition(en). Für groß e Kernradien xc = 2.0 existiert nur jeweils eine (sogenannte) tangential kritische Kurve, die zweite (radial) kritische Kurve ermoglicht das Auftreten `radialer' Arcs oder eines 4 bzw. 5-fach-Bildes.

by In Figur 2.1 kann man ablesen, daß  sich die Anzahl der Bilder einer Quelle immer um zwei ändert, wenn sie eine kritische Linie überschreitet. Man kann allgemein für nicht-singuläre Materieverteilungen beweisen, daß  die Anzahl der Bilder einer Quelle immer ungerade ist (Burke 1981, Schneider 1984, Seitz & Schneider 1992, 1994) und sich daher beim Überschreiten von Kaustiken um Vielfache von zwei ändern muß . Während Figur 2.1 vor allem die Entstehung von Mehrfachbildsystemen und Arcs veranschaulichen soll, zeigt Figur 2.2 typische Bildkonfigurationen für (grob) realistische Modelle für Galaxienhaufen. In den 4 Teilfiguren wird der Kernradius und damit die Steilheit des Massenprofils sowie die Flächenmassendichte im Zentrum der Massenverteilung verändert. Kleine Kernradien begünstigen somit das Auftreten von Mehrfachbildern und Arcs. Die Position von Bildern an einer radial kritischen Linie miß t ungefähr den Kernradius (und damit das Abflachen des Potentials), die Position an einer tangentialen kritischen Linie miß t die Amplitude des Potentials.

Das Singularitätskriterium [ 1-k(q) ]² -| g(q) |² = 0 verdeutlicht, warum die in (2.15) definierte Flächenmassendichte S_crit als kritische Flächenmasendichte bezeichnet wird. Gilt k > 1 an einer beliebigen Position in der Linsenebene, ist das eine Garantie für die Existenz von kritischen Linien und ermöglicht das Auftreten von Mehrfachbildern. Ferner wird deutlich, daß  für eine feste physikalische Flächenmassendichte S die Linsenstärke proportional zu [(D_dsD_d)/( D_s)] ist. Der Wert dieses Faktors hängt von der Hubblekonstante, von der Materiedichte

r = Wr_crit, von der kosmologischen Konstante und den Rotverschiebungen von Quelle und Linse ab. Für feste Quellrotverschiebung existiert eine Linsenrotverschiebung, so daß  [(D_dsD_d)/( D_s)] maximal wird (für eine Quelle bei z_s = 2 ist die optimale Linsenrotverschiebung ungefähr bei z_d » 0.5); für eine Linse bei gegebener Rotverschiebung wird eine Quelle mit `unendlicher' Rotverschiebung am stärksten gelinst.

Aufgaben:
· T6
· T7
· T8

2.3.5 Verstärkung
Der Absolutwert der Determinante der Jacobimatrix, | detA(q) |, beschreibt, wie infinitesimale Raumwinkelelemente von der Linsenebene auf die Quellebene abgebildet werden, d²b = | detA(q) | d²q. Ist die Jacobimatrix nicht singulär, kann man diese Gleichung invertieren und erhält die Raumwinkelgröß e des Bildes in Abhängigkeit vom Raumwinkel der Quelle. Ist

Aufgabe:
· T9

2.4 Die singuläre isotherme Sphäre

Um Linseneffekte qualitativ zu diskutieren, approximiert man häufig die Massenverteilung von Galaxien und Galaxienhaufen durch die einer singulären isothermen Sphäre (SIS). In diesem Modell (Binney & Tremaine 1987) betrachtet man eine Galaxie als ein sphärisch symmetrisches, selbstgravitierendes, ideales Gas der Temperatur T, dessen Gasteilchen aus Sternen (oder stoß freien Elementarteilchen) der Masse m bestehen, die eine Geschwindigkeitsdispersion s = [Ö(k_BT/m)] entlang einer Sichtlinie aufweisen. Man erhält eine einparametrige Schar von Modellen, deren Dichte beim Abstand R vom Zentrum durch r(R) = [(s²)/( 2pG)] [1/( R²)] gegeben ist. Die, für den Ablenkwinkel relevante, projizierte Flächenmassendichte in einem Winkelabstand | q | vom Massenzentrum beträgt

Wie oben diskutiert, markiert der Einsteinradius denjenigen Bereich, in dem die Linse Mehrfachbilder erzeugen kann, oder `kritisch' ist. Unter der Annahme, daß  die Quelle so weit von der Linse entfernt ist, daß  D_ds » D_s gilt, beträgt der Einsteinstradius einer Linse mit der Geschwindigkeitsdispersion von s = 220 km /s ( s = 1000 km/s) 1.4 Bogensekunden (eine halbe Bogenminute). Galaxien sind also (grob) auf einer Skala von Bogensekunden kritisch, bei sehr massiven Galaxienhaufen ist die Winkelskala etwa 30 mal so groß .

Das SIS-Model ist insofern unrealistisch, als daß  die Flächenmassendichte im Zentrum singulär wird, die Gesamtmasse divergiert und Beobachtungen zeigen, daß  die sphärische Symmetrieannahme im allgemeinen nicht gerechtfertigt ist. Es sind daher parametrisierte Linsenmodelle entwickelt worden, die durch Einführung eines Kernradius die Singularität beseitigen, deren Gesamtmasse durch einen steileren Abfall der Flächenmassendichte endlich bleibt und die elliptische Potential- oder Massenkonturen zulassen. (SEF, Fort & Mellier (1994) und dort gegebenene Referenzen).

Dennoch ist das SIS-Modell sehr nützlich, wenn man Linseneigenschaften qualitativ diskutiert und wenn man gemittelte Linseneigenschaften im nichtkritischen Bereich beschreiben will:
i) Die Massenverteilung der Linse wird mit nur einem freien Parameter s beschrieben, der bei bekannter Quell- und Linsenrotverschiebung sofort aus dem Radius eines Einsteinrings abgeleitet werden kann.
ii) Die so abgeleitete `Geschwindigkeitsdispersion' s kann mit anderen Messwerten, wie der Geschwindigkeitsdispersion von Sternen und Gas in Galaxien, oder von Galaxien in Galaxienhaufen verglichen werden.
iii) Ferner zeigen numerische Simulationen der Strukturentstehung (Navarro et al. 1995), daß  kollabierte Objekte wie Galaxien und Galaxienhaufen, wenn man das Zentrum und den äuß eren Bereich ausspart, sehr gut dem Dichteverlauf einer SIS folgen. Man kann daher das SIS-Modell zur Abschätzung der mittleren Verstärkung von einfach abgebildeten Quellen benützen.

Aufgaben:
· T10
· T11
· T12

3 Bestimmung der Massenverteilung einer Gravitationslinse mit Hilfe von Mehrfachbildern

3.1 Die p×Daumenmethode

Wird eine punktförmige Quelle (Quasar) durch eine Gravitationslinse mehrfach abgebildet, so kann man die relativen Positionen der Bilder sowie ihr Fluß verhältnis (das ist gleich ihrem Verstärkungsverhältnis) beobachten. Ist die Quelle räumlich ausgedehnt (Galaxie), so liefern die Größ e und die räumliche Verteilung des Lichts in den Bildern zusätzliche Information: das Größ enverhältnis der Galaxien muß  mit ihrem Fluß verhältnis übereinstimmen, die Lichtverteilung der Bilder muß  in erster Näherung durch eine lineare Transformation ineinander überführbar sein. Mehrfachbilder schränken die Parameter für mögliche Massenverteilungen einer Linse ein. Ein gutes Linsenmodell ist dadurch charakterisiert, daß   alle Bilder auf dieselbe Position in der Quellebene abgebildet werden und daß  der Verstärkungsfaktor an den Bildpositionen für alle Bilder zu einer übereinstimmenden zugehörigen Quellhelligkeit führt. Sind die Bilder ausgedehnt, muß  auß erdem die für jedes Bild berechnete Größ e und Lichtverteilung der Quelle übereinstimmen. Das Fluß - und Größ enverhältnis von Bildern muß  im Rahmen ihrer Fehlergrenzen gleich sein, weil Verstärkung nur durch eine Raumwinkelverzerrung (2.22) verursacht wird. Ist das nicht der Fall, haben die Bilder nicht dieselbe Quelle, oder Staub entlang der Sichtlinie zu einem oder mehreren Bildern verringert den gemessenen Fluß . Mehrfachbilder von Galaxien führen dann zu besonders spektakulären Erscheinungen, wenn sie sich nahekommen und zu einem sog. `luminous arc' verschmelzen. Solche Bilder befinden sich in der unmittelbaren Nähe einer kritischen Kurve und skizzieren ihren Verlauf näherungsweise. Diese Kenntnis kann zu einer einfachen Massenabschätzung der Linse herangezogen werden: wenn man die kritische Linie durch einen Kreis mit Radius q_E approximiert, so gilt für die Masse innerhalb R_E = q_E D_d

Mehrfach abgebildete Galaxien enthalten mehr Information als mehrfach abgebildete Quasare; zudem sind Galaxien bei gleicher Helligkeit sehr viel häufiger als Quasare. Die Entdeckung eines mehrfach abgebildeten Quasars ist jedoch einfacher als die Entdeckung von mehrfach abgebildeten Galaxien. Deswegen war das erste beobachtete Linsensystem ein Doppelquasar (0957+561, Walsh, Carswell & Weynman, 1979), und deswegen konzentrierten sich systematische Suchen nach Linsen im optischen Bereich vor dem Start des Hubble-Space-Telescopes (HST) immer nur auf Quasare als mögliche Quellen.

Aufgaben:
· P1
· P2
· P3
· P4

3.2 Massenbestimmung mit Hilfe eines Linsemodelles - hier für den Galaxienhaufen Cl0024

Im folgenden soll versucht werden, die Eigenschaften des Galaxienhaufes Cl0024 mit einem Modell für sein Ablenkpotential y einzuschränken, das die Bildpositionen A-D reproduziert. Wir verwenden dazu ein sogenanntes elliptisches Potential (die Isopotentialkurven sind Ellipsen) der Form

i)

Für den Fall sphärischer Symmetrie und für Abstände vom Zentrum, die groß  sind relativ zum Kernradius,

ii)

Für kleine Elliptizitäten des Haufenpotential, e_cl < 0.2 , sind auch die Kontouren gleicher Flächenmassendichte näherungsweise Ellipsen und mit der Definition

Aufgaben:
· T13
· P5
· P6
· T14

Für eine quantitativere Analyse benützt man, daß  Mehrfachbilder eine gemeinsame Quellposition besitzen. Man bildet jede Bildposition in die Quellebene ab und ändert die Parameter des Ablenkpotentials so, daß  der gegenseitige Abstand der vom Modell vorhergesagten Quellpositionen minimal wird. Die kopierte Figur (`Figur 5a and b') veranschaulicht die Prozedur.

· P7
· T15
· P8
· P9
· P10
· T16

4 Der Versuch

Hilfestellungen:
· 1
Anschauen eines ps-files: `ghostview file.ps' oder `xv file.ps'. Ausdrucken des ps-files: mit Maus-unterstuetzung von `gh' oder `xv' aus, oder direkt mit `lpr -Plp0 file.ps'.

· 2
Mit `sm' ein ps-file erstellen: `sm -m macroname.sm file' (z.b. `sm -m Prak1.sm file').

· 3
Fortran-Programm z.B. mit `f77 fortranprogramm.f' compelieren.

· 4
Editieren der *.sm sowie prak*_infile*.f mit emacs: `emacs filename &'

Aufgaben:
· T1
Was ergibt sich für den Winkelabstand D(z₁,z₂) in einem Einstein-de Sitter (EdS)-Universum ( W = 1, L = 0)? Für den Speziallfall z₁ = 0 gilt dann D(z) º D(z₁ = 0,z₂ = z) = ??.

· T2
Wie groß  ist die Hubble Länge c/H₀ für eine Hubblekonstante von 100 km/(s  Mpc). Man schreibt allgemein c/H₀ = ?? Mpc   h^-1, dabei ist h = H₀/ 100 km/(s  Mpc). Für eine Hubblekonstante von 40 und 80 km/(s  Mpc) folgt?

· T3
Für die nächsten beiden Punkte wird W = 1 und L = 0 angenommen. Ein Beobachter bei z₁ = 0 beobachtet eine Struktur (Galaxie, Galaxienhaufen) bei der Rotverschiebung z = z₁ mit einer Ausdehnung Dq. Für die Größ e Dx dieser Struktur folgt mit der Definition der Winkeldistanz Dx = D(z) Dq. Wieviel kpc bzw. Mpc entspricht eine Bogensekunde bzw. eine Bogenminute bei der Rotverschiebung z = 0.4? Vorsicht! Für die Multiplikation muß  der Winkel vom Gradmaß  in Steradian umgerechnet werden! Ein typischer Galaxienhaufen hat einen (Abell)-Radius von 1.5 Mpc h^-1. Welchen Winkel durchmesser hat damit ein typischer Haufen bei einer Rotverschiebung von z = 0.2, z = 0.4, z = 1.0 und z = 1.5?

· T4
Ein Beobachter habe folgende drei Kameras zur Verfügung: WFPC-2 am HST (Seitenlänge 1600 Pixel mit einer Skala von 0¢¢.1/Pixel), EMMI am ESO-NTT, (Seitenlänge 2048 Pixel und 0¢¢.27/Pixel) und die UH8K am CHFT (Seitenlänge 8192 Pixel also `8K' und 0¢¢.2/Pixel). Welches Gesichtsfeld (Field of View = FOV) überdecken diese drei Kameras, und wie groß  sind die Strukturen, die man maximal bei einer Rotverschiebung von 0.1, 0.4 und 1.0 abbilden kann? Mit welcher Kamera würdest Du am liebsten Mehrfachbilder in Galaxien und Arcs in Galaxienhaufen beobachten, warum?

· T5
Der Ablenkwinkel in einer Entfernung b einer Punktmasse M mit Scharzschildradius R_s = 2 GM/c² beträgt

· T6
Rechne (2.15) nach. Tip für solche, die sich den Wert von G nicht merken können: 4G/c² = 2 ( 2 G M_\sun /c² ) M^-1_\sun = 2 R_s,\sunM^-1_\sun .

· T7
Nach (2.15) hängt die Stärke einer Linse nicht nur von ihrer Flächenmassendichte, sondern auch von der relativen Anordnung des Beobachters, der Linse und der Quelle ab, es gilt k µ D_d D_ds / D_s. Benütze das zur Verfügung gestellte Programm (prak1.f, Quellrotverschiebung, kosmologische Parameter und Name des Outputfiles werden in prak1_infile.f festgelegt), um die geometrische Linsenstärke D_d D_ds / D_s für eine Linsenrotverschiebung von z = 0.2, 0.4, 1.0 in Abhängigkeit der Quellrotverschiebung z_s zu berechnen. Führe diese Berechnung für ein EdS-Universum und für den Fall W = 0.3,

L = 0, sowie W = 0.3, L = 0.7 durch.

· T8
Die Wahrscheinlichkeit für das Auftreten einer bestimmten Linsenkonfiguration hängt nicht nur von der (geometrischen) Stärke einer Linse ab, sondern auch von der Häufigkeit der Linsen. Unter der Annahme, daß  sich die Dichte von Linsen (z.B. Galaxien) nur durch ihre Expansion ändert, gilt für ihre Anzahl bei der Rotverschiebung z (pro Raumwinkel und Rotverschiebungsintervall): N µ (1+z)³   D²(z)×dr_proper/dz. Für welche kosmologischen Parameter erwartet man am meisten solcher Linsensysteme?

· T9
Die Flächenmassendichte und Scherung sind beide zweite Ableitungen des Ablenkpotentials. Und für schwache Linsen mit k << 1 gilt g: = | g | » k. Was folgt in dieser Näherung für den Verstärkungsfaktor?

· T10
Berechne b: = 4p(( s)/ c )² in Bogensekunden für eine Galaxie mit einer Geschwindigkeitsdispersion von

s = 220km/s und Galaxienhaufen mit s = 800, 1000 und 1200 km/s.

· T11
Für die Linsenstärke einer SIS ist wegen (2.23) nicht nur ihre Geschwindigkeitsdispersion sondern auch die relative Anordnung von Beobachter, Linse und Quelle verantwortlich. Untersuche die Monotonie von D_ds/D_s für ein Einstein-de Sitter Universums als Funktion der Quellrotverschiebung. Welchen Wert hat dieser Quotient für z_s ® ¥?

· T12
Berechne diesen Quotient mit Hilfe des zur Verfügung gestellten Programms (prak2.f, Linsenrotverschiebung, kosmologische Parameter und Name des Outputfiles werden in prak2_infile.f festgelegt), für Linsenrotverschiebungen von z_d = 0.2, 0.4 und z_d = 0.8 für dieselben Parametersätze von W und L wie in 2.3.2. Wie gut gilt im EdS-Fall für z_s = 4 der oben abgeleitete Grenzwert?

· P1
Betrachte den Galaxienhaufen Cl0024+1654, der sich bei einer Rotverschiebung z_d = 0.39 » 0.4 befindet, mit `saoimage' (Aufruf `saoimage Cl0024_I_hst.fits &'). Diese Aufnahme wurde mit dem HST im I-Band (FW814-Filter) erhalten. In der Nähe des Zentrum des Galaxienhaufens (auf dem 3. Chip der Kamera) ist eine vierfach abgebildete Q-förmige Galaxie zu sehen. Gefunden? Welcher der in Figur 2 gezeigten Bildkonfigurationen entspricht die des Vierfachbildes in Cl0024 am ehesten? Findest Du auch das fünfte Bild?

· P2
Vergleiche die HST Aufnahme mit der CHFT-Aufnahme (180 min im B-Filter), die unter hervorragenden Bedingungen (`Seeing' der koaddierten Bilder ist 0¢¢.7) erhalten wurde. Wo ist im HST-Bild Norden? Im folgenden wird die in dieser Figur eingeführte Nomenklatur beibehalten.

· P3
Bestimme aus dem Bild ganz grob den Abstand von C, B und A und des Gegenbildes D zum Haufenzentrum (in Pixeln). Notiere dazu vorher `die' Bildpositionen für C, B, A und D in Pixeln. Die Bilder sind ausgedehnt. Welche Teile der Quelle entsprechen einander in den verschiedenen Bildern? Was nimmst Du folglich als `die' Bildposition? Findest Du auch das fünfte Bild? Diskutiere in der Ausarbeitung (Vergleich mit Figur 2.2) auch, wo Du das fünfte Bild erwartest! Betrachte jetzt zum Vergleich das Farbbild (B-I-Farben!) von Cl0024 (blaue/rote Objekte sind blau/rot in ihrer spektralen Energieverteilung), es wird mit `xv cl024_color.gif' aufgerufen. Falls Du das fünfte Bild bis jetzt noch nicht identifiziert hast, kannst Du jetzt das mit E bezeichnete Objekt in dem dem Cl0024_I_hst.fits-file finden.

Bilde Schätzwerte für den Einsteinradius in Bogensekunden (ein Pixel entpricht 0¢¢.1). Was erhält man, wenn man den Abstand zwischen B und D als Durchmesser für den Einsteinkreis interpretiert? Welche Geschwindigkeitsdispersion des Galaxienhaufens kann man daraus (für eine SIS) ableiten? (Nimm W = 1, L = 0 an. Verwende für die Quellrotverschiebung einmal z_s® ¥ bzw. z_s = 1.6). Vergleiche die Differenz der oben abgeleiteten Geschwindigkeitsdispersionen mit dem Fehler, den Du (nach dem Fehlerfortplanzungsgesetz aufgrund der ungenauen Messung der Bilderpositionen und des Haufenzentrums erwartest. Verwende dazu einmal Dq_E = 0¢¢.1 sowie 1¢¢.0.

Berechne für obige Fälle die im Einsteinradius eingeschlossene Gesamtmasse. Wie groß  ist der Einsteinradius in kpc h^-1?

· P4
Wenn man das Modell in Figur 2 zugrunde legt, welche obere Grenze für den Kernradius des Galaxienhaufens kann man dann ableiten? Kann man diese Abschätzung noch aufrechterhalten, wenn man die Masse der zentralen Galaxien berücksichtigt?

· T13
Rechne (3.4)-(3.6) nach.

· P5
Nimm an, daß  das Haufenzentrum mit dem Maximum der Lichtverteilung der zentralen Galaxie (CG2) in Cl0024 übereinstimmt. Wie genau kann man diese Position aus dem Bild `raten'? Verwende im folgenden als Haufenzentrum diejenige Position, die SExtractor-Software für diese Galaxie liefert: x_HST^CG2 = 1206.6 und y_HST^CG2 = 389.7.

· P6
Führe dieselbe Schätzung für die Galaxien G1 und G2 durch. SExtractor liefert für G1 und G2 die Werte x_HST^G1 = 1122.1 und y_HST^G1 = 699.3 bzw. x_HST^G2 = 1067.8 und y_HST^G2 = 746.3. Mich hat zunächst die y-Position von G1 überrascht. Dich auch?

· T14
Das Ablenkpotential (3.2) besitzt vier freie Parameter. Einen Winkel f (für die Transformation vom HST-Koordinatensystem in das

· P7
Das Programm `prak3.f' minimiert für (in gewissen Rahmen) wählbare freie Parameter den Abstand von A,B,C und D (und Subkonfigurationen) in der Quellebene. Beschreibe die Linse zunächst nur durch den Galaxienhaufen und lasse alle Parameter im wesentlichen ohne Einschränkung variieren (prak3_in1.f). Betrachte die ungefähr vorhergesagten Mehrfachbildsysteme. Es fällt auf, daß  vor allem B viel zu `lang' vorhergesagt wird. An welcher Vereinfachung kann das liegen?

· T15
Die Galaxien G1 und G2 müssen - wenn sie Masse besitzen - einen Einfluß  auf die Bildpositionen und Ausdehnung der Bilder haben. Warum ist B am stärksten betroffen und warum hat eine Masse den größ ten störenden Einfluß , wenn sie sich in der Nähe einer kritischen Linie befindet?

· P8
Es sei nun die Masse von G1 und G2 zugelassen aber festgehalten (einmal mit 126 und 137 km/s - das ist ein Schätzwert von einer ähnlichen Studie von Kassiola, Kovner & Dantel Fort (1994)- und einmal mit jeweils 210 km/s - dies ist ein Schätzwert aufgrund der Faber-Jackson Relation). Beobachte wie sich die Form der Kuspe durch die Störung ändert (verwende dazu prak3_in2.f und prak3_in3.f).

· P9
Vergleiche die relative Orientierung der `Farbkleckse' mit der relativen Orientierung, die man aus der Q-Quelle ableiten kann. Jeweils zwei der vier helleren Bilder haben eine `positive' bzw. `negative' Parität (Händigkeit). Zeichne die Bilder C, B, und A qualitativ in die Ausarbeitung und zeichne ein, welche Punkte in C und B einander entsprechen. Welche Parität besitzt das fünfte Bild (E)?

· P10
in prak3_in4.f können die Galaxien G1 und G2 eine beliebige Geschwindigkeitsdispersion annehmen zwischen 100 und 300 km/s annehmen. Probier am Schluß  aus wie stabil die Reproduktion der Vierfachbilder ist und wie eindeutig (?) die `best'-fit parameter sind, indem du z.B. eine obere Grenze für den Kernradius (20 oder 30 Pixel) oder eine untere Grenze für die Elliptizität (0.04) einführst oder die Haufenposition als freie Parameter betrachtest. Verwende dazu prak3_inplay.f. Welcher Haufenparameter ist am besten festgelegt?

· T16
In unserem einfachen Modell werden nur `die' Positionen der vier Bilder als Observablen verwendet. Wie kann man das im Prinzip besser machen?

Referenzen

Binney, J. & Tremaine, S.  1987, Galactic dynamics, Princeton University Press, Princeton.

Blandford, R.D. & Narayan, R. 1986, APJ, 310 568.

Börner, G. 1988, The early universe, Springer, Heidelberg.

Fort, B. & Mellier, Y.  1994, A&AR, 239, 5.

Fukagita, M., Futamase, T., Kasai, M. & Turner, E.  1992, APJ, 393, 3.

Kaiser, N. & Squires, G. 1993, ApJ, 404, 441 (KS).

Kochanek, C.S. 1995, APJ, 453, 545.

Kundic et al. 1996, preprint

Lynds, R. & Petrosion, V.  1986, BAAS 18, 1014.

Mattig, W.  1958, Astron. Nachr., 284, 109.

Padmanabhan, T.  1993, The large scale structure of the universe, Cambridge University Press.

Pazcy\' nsky, B. 1986, APJ, 304, 1.

Peebles, P. J. E.  1993 Principles of Physical Cosmology, Princeton University Press.

Refsdal, S.  1964, MNRAS, 128, 307.

Schneider, P.  1984, A&A, 140, 119.

Schneider, P., Ehlers, J. & Falco, E.E.  1992, Gravitational Lenses, Springer-Verlag.

Seitz, S., Schneider, P.  1992, A&A, 265, 1.

Seitz, S.  1993, Diplomarbeit, Ludwig Maximilian Universität München.

Seitz, S., Schneider, P. & Ehlers, J.  1994, Class. Quantum Grav., 11, 2345.

Seitz, S. & Schneider, P.  1994, A&A, 287, 349.

Soucail, G., Mellier, Y., Fort, B., Hammer, F. & Mathez, G.  1987, A&A, 172, L14.

Walsh, D., Carswell, R.F. & Weynman, R.J.  1979, Nat. 279, 381.

Weinberg, S.  1972, Gravitation and Cosmology, John Wiley & Sons.