Research interests

Observations of cosmic large-scale structure have emerged as some of the richest probes for cosmology over the past few decades. Galaxy redshift-surveys are exploring ever larger fractions of the observable Universe and reveal it to be remarkably isotropic and homogeneous. Only on scales below ∼ 100 Mpc they find more complicated structures, known as the cosmic web consisting of gravitationally bound arrangements of dark matter, such as halos, filaments and sheets, which themselves host galaxies. Their statistical composition and spatial distribution contains a plethora of information about the origin and evolution of the Universe, but due to the nonlinear and stochastic nature of structure formation it is difficult to infer its underlying physical laws and parameters. Thanks to substantial efforts in theoretical and numerical studies, this task has become more and more procurable in modern-day cosmology. For the next generation of planned experiments, unprecedented precision measurements will demand firm predictions from theory. My aim is to tackle open problems in cosmology using either analytical, numerical, or observational methods. I am particularly interested in investigating the nature of dark energy and dark matter, measuring cosmological parameters, and testing Einstein's General Relativity (GR). Among the relevant observational missions in this field are both completed and planned experiments, such as BOSS, DES, EUCLID, LSST, and The Roman Space Telescope. Brief descriptions of some selected research projects I have been involved in are listed below.

Cosmic Voids

The dominant volume fraction of the Universe consists of relatively empty space, so-called cosmic voids. This is a simple consequence of gravitational clustering, which always acts to enhance over-dense structures via collapse, while under-densities are depleted and expand. With the advance of modern galaxy surveys reaching the necessary sky coverage and depth to reveal the cosmic web, studies on voids have augmented rapidly in the current literature. Recently, both observations and simulations have been analyzed to quantify various properties of voids, such as their abundance, their density and velocity structure (see Fig. 1), their ellipticity distribution, and their clustering statistics. It has been demonstrated that voids can teach us a great deal about the composition of large-scale structure and its evolution, and that they can be well described by simple empirical models. For example, it has been shown that the relation between density and velocity profiles of voids largely follows linear theory [1], that they are surrounded by over-dense compensation walls determining their dynamics, and that some of them are doomed to collapse (voids in clouds), while others grow forever with super-Hubble expansion rates (voids in voids) [2]. Moreover, this dichotomy defines a unique class of compensated voids whose net mass deficit inside is precisely balanced by their surrounding compensation wall. This gives rise to some interesting properties, such as the definition of a static cosmological ruler [3].

My aim is to develop a deeper understanding on the various properties of voids, using both numerical and observational datasets to compare with theoretical predictions. There are still many open questions regarding how to relate these properties to the initial conditions of the Universe and how to derive them from first principles. In turn, this will be beneficial for utilizing voids as probes for cosmology and fundamental physics, as is discussed in the following subsections.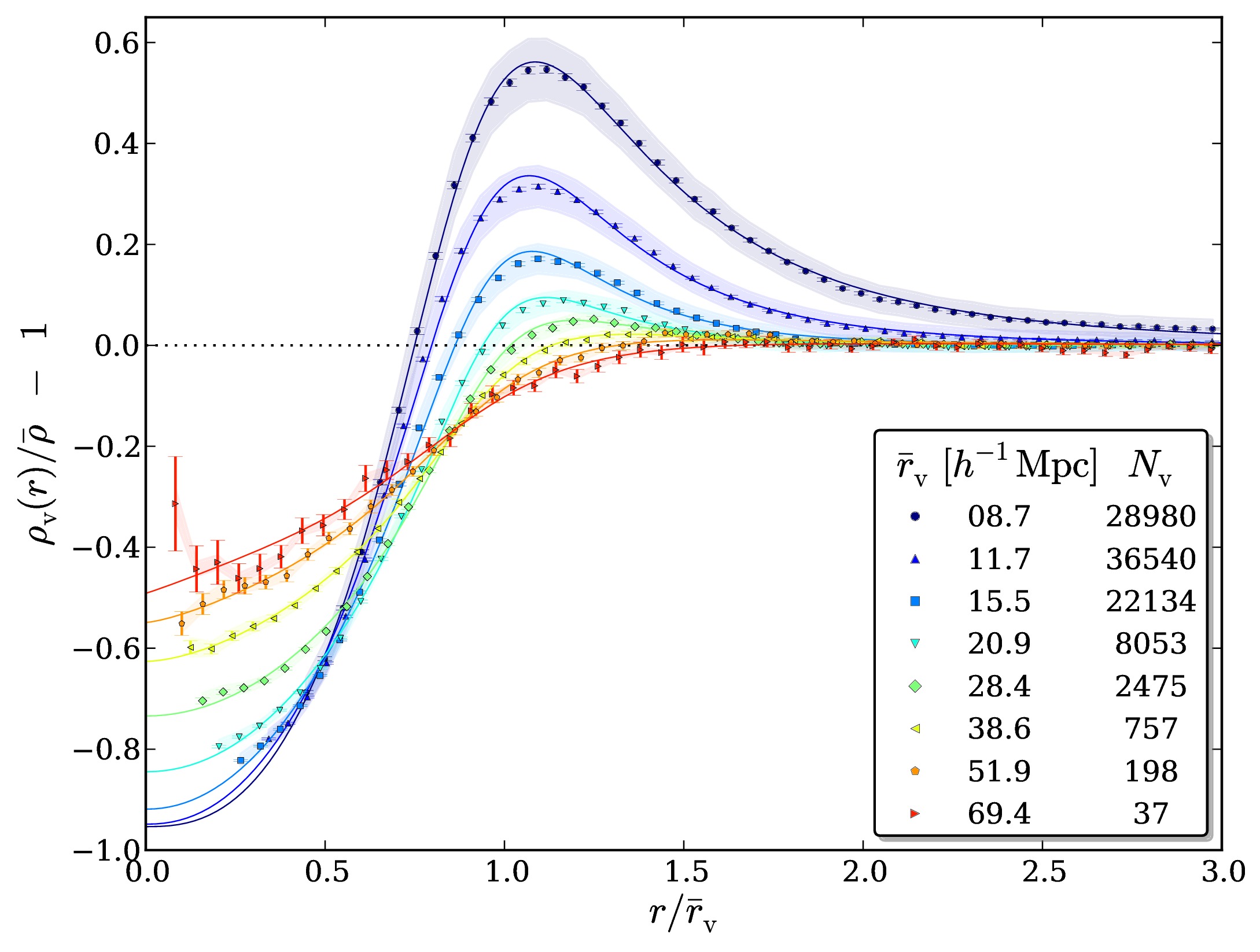

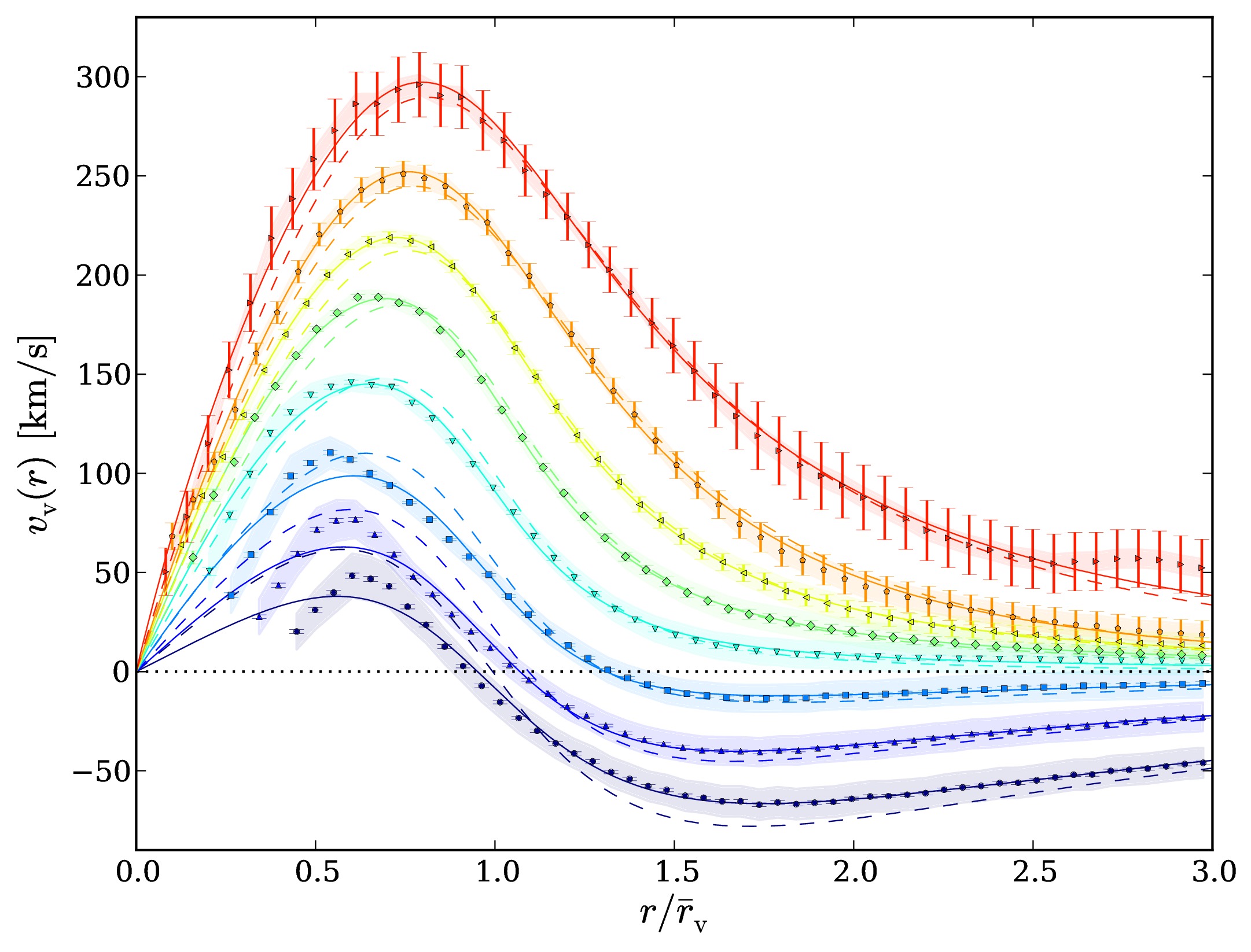
Fig. 1: Density and velocity profiles of voids found in a ΛCDM N-body simulation [1].

Dark Energy – Because GR relates the distribution of matter and energy to the geometry of spacetime via Einstein's field equations, observations of the cosmic expansion history allow constraining the material constituents of our Universe. In this manner supernova distance measurements have inferred an exotic form of dark energy (respectively a cosmological constant) that appears to dominate the cosmic energy budget today and is responsible for the Universe's accelerated expansion. A particularly elegant method to probe the cosmic expansion history has been proposed by Alcock and Paczynski (AP) in 1979 [4]. It is based on the cosmological principle, stating the Universe obeys statistical homogeneity and isotropy. Geometric distortions can thus only be caused by coordinate transformations that assume a wrong cosmology. Galaxy redshift surveys offer ideal means to perform a so-called AP-test, as they are able to map out the 3D distribution of matter in large cosmological volumes.

An alternative observable to the distribution of galaxies for carrying out an AP-test is the shape of stacked voids [5, 6, 7]. Voids are the most dark energy dominated structures in the Universe, as their matter density is very low by definition. In practice, stacked voids are constructed by alignment of their center and by counting galaxies around it. This is equivalent to the void-galaxy cross-correlation function and hence a two-point statistic like the galaxy correlation function (see Fig. 2). However, voids have the advantage of being the least evolved structures in the Universe, which makes their theoretical description more feasible and easier relate to its initial conditions [8]. In contrast to galaxy correlations, which are quadratic in the density of galaxies, void-galaxy cross-correlations merely depend on galaxy density linearly. Nonlinear contributions from galaxy peculiar motions (redshift-space distortions) are less severe in this case, allowing to extend the available range of scales for modeling the observational data. Another statistic adequate for an AP-test is the void auto-correlation [9]. In contrast to the other two methods, this statistic is not directly affected by redshift-space distortions at all, as the galaxy density does not enter in it. Galaxy peculiar motions only affect it indirectly when voids are identified in redshift space, but the net displacement of the void center is small in this case.

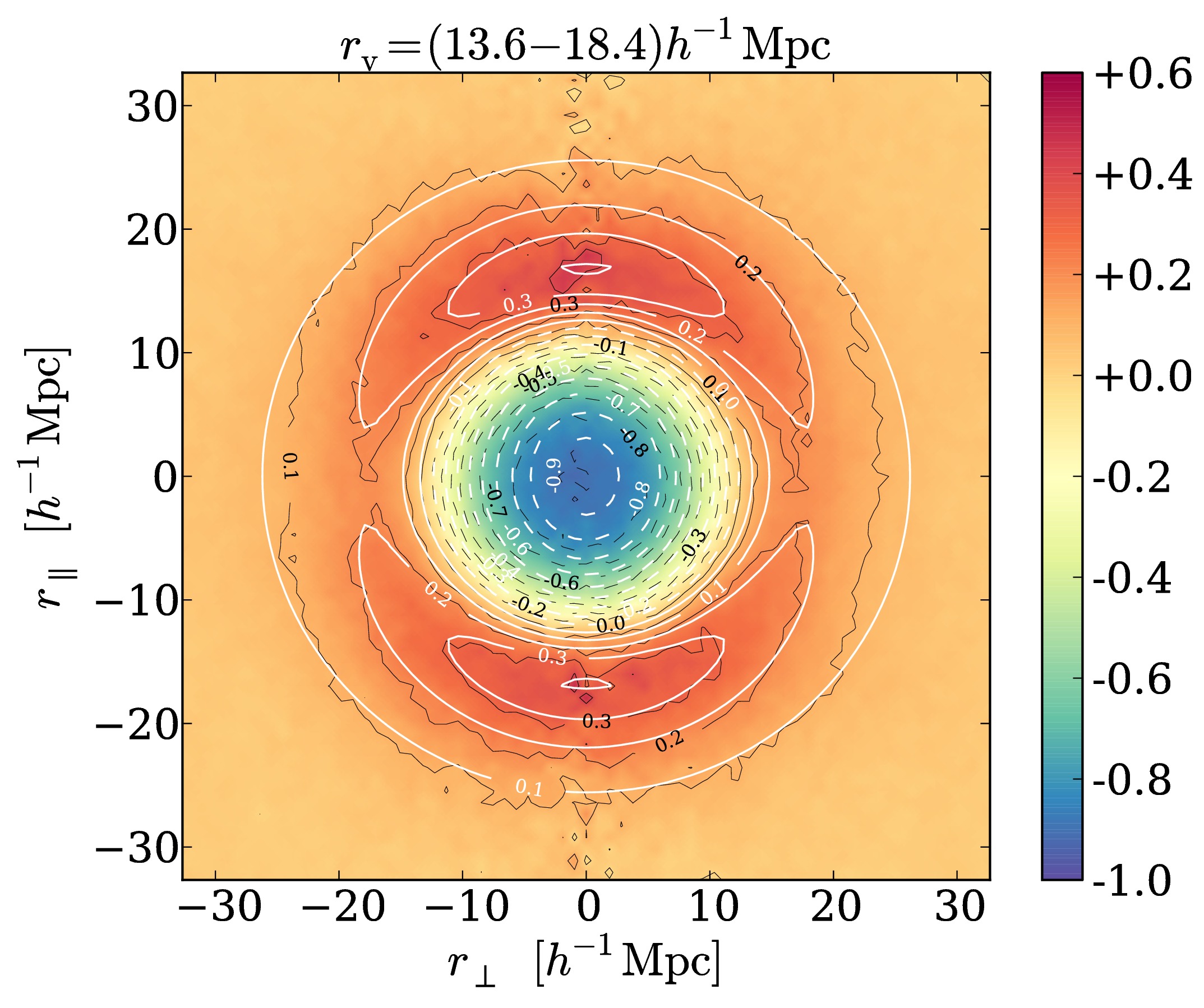
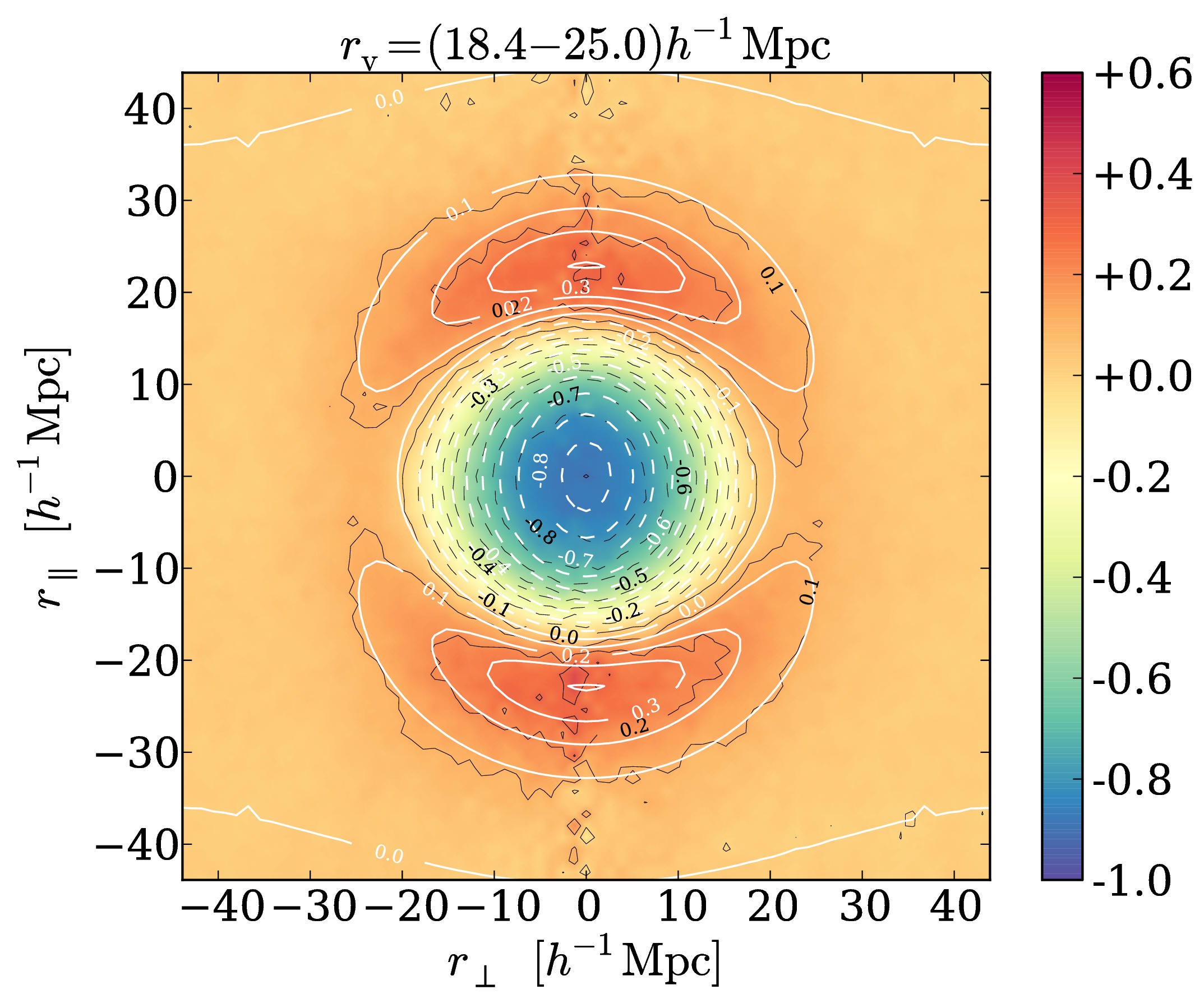
Fig. 2: Void-galaxy cross-correlation functions from a mock-galaxy catalog in redshift space [7].

For future analyses of observational data, a framework that allows accounting for all the three above mentioned statistics at the same time could prove beneficial. Conducting a combined study of geometric and dynamic distortions will have the potential to tighten our current constraints on the expansion history of the Universe and its cosmological parameters, while having better control over their systematics. In turn, this may help to shed light on the nature of dark energy (its equation of state) and the validity of GR on very large scales [10].

Dark Matter – In numerical simulations the structure of cosmic voids is commonly analyzed under minimal assumptions about the properties of hypothetical dark matter particles, which are thought to dominate the matter content of our Universe. In particular, they are often assumed to be cold, i.e. not to possess any thermal energy. Furthermore, other potential influences from neutrinos or baryons are usually being neglected. However, relaxing these assumptions will likely have an effect on various characteristics of voids, such as their density profile, abundance, or ellipticity, for example. These open questions can be tackled by analyzing non-standard simulations for their detailed void properties, and by comparing the results to expectations from theory. The ultimate goal for this endeavor is the application of the acquired results to observational data and to be able to constrain properties of the dark matter particle, or the total mass of all neutrino species, for example.

While gravitational (anti)lensing observations give a direct estimate on the distribution of dark matter inside voids [11], the 3D distribution of galaxies may be considered for the same purpose. Recent studies have investigated the relation between voids identified in dark matter and in the distribution of galaxies [12]. They find universal characteristics for voids, regardless the type of tracer used to identify them. Thanks to the self-similar nature of large-scale structure, simple scaling laws can translate void properties from one tracer to another, allowing a direct interpretation of the observational data.

Inflation – The current standard model of cosmology relies on the idea that the Universe must have undergone a period of exponentially rapid expansion shortly after the Big Bang, a theory referred to as inflation. While this idea explains the high degree of homogeneity and flatness of the cosmos, its underlying physics is poorly constrained. The simplest models assume a single scalar field of yet unknown origin to cause the driving force of inflation, but hundreds of alternative models involving multiple different fields, as well as alternatives to inflation, such as the ekpyrotic scenario, have been proposed in the literature. One important observable to potentially distinguish these different models is the deviation from Gaussianity in the statistics of density fluctuations in the Universe. So far the cosmic microwave background has provided the tightest bounds on so-called primordial non-Gaussianity, but recent observations of large-scale structure using galaxy surveys have demonstrated to be able to yield comparable, if not potentially better constraints [13, 14].

In comparison to galaxies, respectively their host halos, cosmic voids are more closely related to the initial conditions of the Universe. On the one hand this is due to the limited number of dark matter phase-space foldings occurring inside them [8, 15], and therefore less violent virialization. On the other hand it is thanks to their relatively quiet merger history [16] that makes voids a pristine tracer of the initial conditions of the Universe even on large scales.

Gravity – Einstein's theory of gravity constitutes one of the most profound and well-tested foundations of modern physics. It is able to successfully describe the dynamical Universe on scales from planetary systems all the way up to the cosmic microwave background. While numerous alternatives and extensions have been developed, GR has so far prevailed its validity and passed all observational tests. One of the weaknesses of common theories for the modification of gravity is the fact that they automatically revert to standard GR in regions of high density (referred to as screening mechanisms, such as Chameleon or Vainshtein), which are commonly the observed ones due to their high detectability. On the other hand, cosmic voids offer a new territory for precision tests of GR in the unprobed regime of low density. There are early indications from analytical calculations [17, 18] and simulations [19, 20] that the interiors of voids may indeed be a smoking gun to look for modifications of GR, but more detailed studies have to be conducted in order to understand their implications.

References

[1] Hamaus, N., Sutter, P. M. & Wandelt, B. D. "Universal Density Profile for Cosmic Voids". Phys. Rev. Lett. 112, 251302 (2014).

[2] Sheth, R. K. & van de Weygaert, R. "A hierarchy of voids: much ado about nothing". MNRAS 350, 517–538 (2004).

[3] Hamaus, N., Wandelt, B. D., Sutter, P. M., Lavaux, G. & Warren, M. S. "Cosmology with Void-Galaxy Correlations". Phys. Rev. Lett. 112, 041304 (2014).

[4] Alcock, C. & Paczynski, B. "An evolution free test for non-zero cosmological constant". Nature 281, 358 (1979).

[5] Lavaux, G. & Wandelt, B. D. "Precision Cosmography with Stacked Voids." ApJ 754, 109 (2012).

[6] Sutter, P. M., Lavaux, G., Wandelt, B. D. & Weinberg, D. H. "A First Application of the Alcock-Paczynski Test to Stacked Cosmic Voids". ApJ 761, 187 (2012).

[7] Hamaus, N., Sutter, P. M., Lavaux, G., & Wandelt, B. D. "Probing cosmology and gravity with redshift-space distortions around voids". JCAP 11, 036, November (2015).

[8] Neyrinck, M. C. & Yang, L. F. "Ringing the initial Universe: the response of overdensity and transformed-density power spectra to initial spikes". MNRAS 433, 1628–1633 (2013).

[9] Hamaus, N., Sutter, P. M., Lavaux, G., & Wandelt, B. D. "Testing cosmic geometry without dynamic distortions using voids". JCAP 12, 013, December (2014).

[10] Yoo, J., Hamaus, N., Seljak, U. & Zaldarriaga, M. "Going beyond the Kaiser redshift-space distortion formula: A full general relativistic account of the effects and their detectability in galaxy clustering". Phys. Rev. D 86, 063514 (2012).

[11] Melchior, P., Sutter, P. M., Sheldon, E. S., Krause, E. & Wandelt, B. D. "First measurement of gravitational lensing by cosmic voids in SDSS". MNRAS 440, 2922–2927 (2014).

[12] Sutter, P. M. et al. "Sparse sampling, galaxy bias, and voids". MNRAS 442, 462–471 (2014).

[13] Slosar, A., Hirata, C., Seljak, U., Ho, S. & Padmanabhan, N. "Constraints on local primordial non-Gaussianity from large scale structure". JCAP 8, 031 (2008).

[14] Hamaus, N., Seljak, U. & Desjacques, V. "Optimal constraints on local primordial non-Gaussianity from the two-point statistics of large-scale structure". Phys. Rev. D 84, 083509 (2011).

[15] Abel, T., Hahn, O. & Kähler, R. "Tracing the dark matter sheet in phase space". MNRAS 427, 61–76 (2012).

[16] Sutter, P. M. et al. "The life and death of cosmic voids". MNRAS 445, 1235–1244 (2014).

[17] Clampitt, J., Cai, Y.-C. & Li, B. "Voids in modified gravity: excursion set predictions". MNRAS 431, 749–766 (2013).

[18] Spolyar, D., Sahlén, M. & Silk, J. "Topology and Dark Energy: Testing Gravity in Voids". Phys. Rev. Lett. 111, 241103 (2013).

[19] Cai, Y.-C., Padilla, N. & Li, B. "Testing Gravity using Cosmic Voids". MNRAS 451, 1036–1055 (2015).

[20] Zivick, P., Sutter, P. M., Wandelt, B. D., Li, B., & Lam, T. Y. "Using cosmic voids to distinguish f(R) gravity in future galaxy surveys". MNRAS 451, 4215–4222 (2014).

Large-Scale Structure

The Galactic Center Black Hole