The Treatment of Line Blanketing

The effect of line absorption and emission on the temperature structure is usually referred to as line blanketing. Although the processes involved are complex, they always increase the Rosseland optical depth ( $\tau_{\rm Ross}^{}$ ). In deeper layers ( $\tau_{\rm Ross}^{}$ > 0.1), where true absorptive processes dominate, this leads directly to an enhancement of the temperature, since in this part the temperature is primarily determined by $\tau_{\rm Ross}^{}$ .

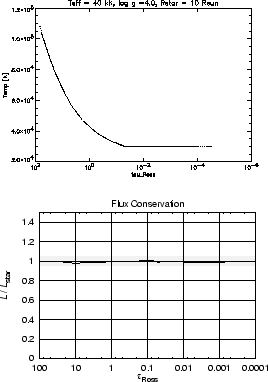
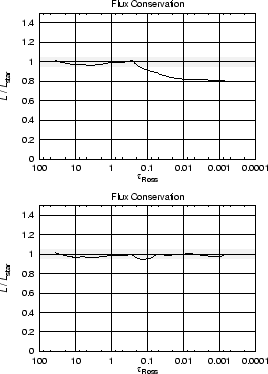
Thus, if we neglect the influence of the metals in a first step, the temperature structure can be easily calculated using the concept of non-LTE Hopf functions (cf. Santolaya-Rey et al. 1997). These functions are based on a parameterization of the temperature stratification obtained from radiative-equilibrium calculations of hydrostatic, plane-parallel H and He non-LTE models, and have been adapted to the spherical case. Fig. 5 shows for an O-dwarf model (henceforth O40; T_eff = 40 000 K), that this method leads to almost identical results for the temperature structures obtained by two completely independent codes. The reliability of this method is further proven by the resulting flux conservation which, as shown on the lower panel of Fig. 5, is on the 1% level. Below we will show that the method can also be extended in order to account for the influence of spectral lines (i.e.,line blanketing).

In the outer part of the expanding atmosphere ( $\tau_{\rm Ross}^{}$ < 0.1), where scattering processes start to dominate, the effect of line absorption and emission on the temperature structure is more difficult to treat. In principle, there are two possibilities: either one calculates for radiative equilibrium, or for balanced heating and cooling rates where all processes have to be included - bound-free, free-free, and collisions. As the $\tau_{\rm Ross}^{}$ values are small in this part, and hence most frequency ranges are optically thin, the latter method turned out to be more suitable.

Figure 5: Temperature structure for a pure H/He O40 model without blanketing. Upper panel: comparison of temperature structures - our model, fully drawn; Puls et al. (XXX1997), dotted. Lower panel: flux conservation (shown is the calculated luminosity divided by the conserved value) for our model.

$\begin{figure} \centerline {\hbox{ \psfig{file=11-T-jo-adi-d40.ps,height=6.5cm}... ...fig{file=12-s50ftulu3Jun6-10-2-12.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

In order to get an impression of the influence of the blanketing effect, we performed a first simulation for the O40 model where line blocking, but not blanketing, was treated (i.e.,we fixed the non-LTE Hopf function).

**Figure 5:** Temperature structure for a pure H/He O40 model without blanketing. *Upper panel:* comparison of temperature structures - our model, fully drawn; Puls et al. (XXX1997), dotted. Lower panel: flux conservation (shown is the calculated luminosity divided by the conserved value) for our model.
$\begin{figure} \centerline {\hbox{ \psfig{file=11-T-jo-adi-d40.ps,height=6.5cm}... ...fig{file=12-s50ftulu3Jun6-10-2-12.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

Figure 6: Flux conservation for an O40 model. Upper panel: blocking effects, but not blanketing effects, are included; Lower panel: both effects are treated consistently

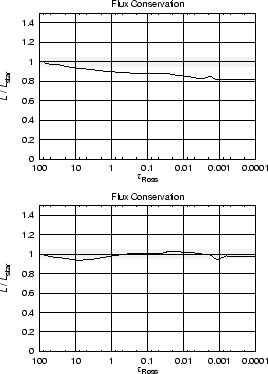$\begin{figure} \centerline {\hbox{ \psfig{file=14-d40f-2-2-16.ps,angle=-90,tota... ...box{ \psfig{file=15-d40f-11-2-14.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

**Figure 6:** Flux conservation for an O40 model. *Upper panel:* blocking effects, but not blanketing effects, are included; *Lower panel:* both effects are treated consistently
$\begin{figure} \centerline {\hbox{ \psfig{file=14-d40f-2-2-16.ps,angle=-90,tota... ...box{ \psfig{file=15-d40f-11-2-14.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

As displayed in Fig. 6, we found a flux deviation which already starts in the inner part, $\tau_{\rm Ross}^{}$ < 50, and reaches a value of 15% at $\tau_{\rm Ross}^{}$ = 0.1. (We note that this is not the worst case; for some supergiant models we obtained flux deviations of up to 50%.) This clearly shows the importance of blanketing effects and the need to correctly account for them. Moreover, from these calculations it turns out that absorptive line opacities dominate the total opacity down to an optical depth of $\tau_{\rm Ross}^{}$ > 0.1 (see also below - Fig. 8). This result is somewhat in contradiction to Schaerer & Schmutz (1994), who found the dominance of scattering opacities over absorptive opacities even at these depths. However, their finding is misleading since their absorptive opacities include only continuum absorption, whereas true line absorption processes are neglected.

Figure 7: Upper panel: temperature structure for the final O40 model where blocking and blanketing effects are included; Lower panel: mismatch of the heating and cooling rates for the same model.

$\begin{figure} \centerline {\hbox{ \psfig{file=16a-T-d40f-11-2-14+d40t_1_t1ni1h... ...{ \psfig{file=17-HC-d40f-11-2-14.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

**Figure 7:** *Upper panel:* temperature structure for the final O40 model where blocking and blanketing effects are included; *Lower panel:* mismatch of the heating and cooling rates for the same model.
$\begin{figure} \centerline {\hbox{ \psfig{file=16a-T-d40f-11-2-14+d40t_1_t1ni1h... ...{ \psfig{file=17-HC-d40f-11-2-14.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

Figure: Comparison of EUV spectra from our models and plane-parallel LTE models of Kurucz. The upper panel shows the spectrum of our final O40 dwarf model ( T_eff = 40 000 K, log g = 4.0) and the emergent fluxes from Kurucz ( T_eff = 40 000 K, log g = 4.5). The lower panel shows the spectrum of our O50 supergiant model ( T_eff = 50 000 K, log g = 3.8) and the emergent fluxes from Kurucz ( T_eff = 50 000 K, log g = 5.0).

$\begin{figure} \centerline {\hbox{ \psfig{file=18-d40k.ps,angle=-90,width=12cm}}}\centerline {\hbox{ \psfig{file=19-s50k.ps,angle=-90,width=12cm}}}\end{figure}$

**Figure:** Comparison of EUV spectra from our models and plane-parallel LTE models of Kurucz. The upper panel shows the spectrum of our final O40 dwarf model ( T_eff = 40 000 K, log g = 4.0) and the emergent fluxes from Kurucz ( T_eff = 40 000 K, log g = 4.5). The lower panel shows the spectrum of our O50 supergiant model ( T_eff = 50 000 K, log g = 3.8) and the emergent fluxes from Kurucz ( T_eff = 50 000 K, log g = 5.0).
$\begin{figure} \centerline {\hbox{ \psfig{file=18-d40k.ps,angle=-90,width=12cm}}}\centerline {\hbox{ \psfig{file=19-s50k.ps,angle=-90,width=12cm}}}\end{figure}$

Figure 9: Flux conservation for an O50 model. Upper panel: not corrected for self-shadowing; Lower panel: corrected for self-shadowing.

$\begin{figure} \centerline {\hbox{ \psfig{file=20b-s50ftulu7g-10-2-15.ps,angle=... ...\psfig{file=21-s50ftulu7a-10-2-12.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

**Figure 9:** Flux conservation for an O50 model. *Upper panel:* not corrected for self-shadowing; *Lower panel:* corrected for self-shadowing.
$\begin{figure} \centerline {\hbox{ \psfig{file=20b-s50ftulu7g-10-2-15.ps,angle=... ...\psfig{file=21-s50ftulu7a-10-2-12.ps,angle=-90,totalheight=6.75cm}}}\end{figure}$

Figure: Schematic sketch to illustrate the problem of self-shadowing (symbols are explained in the text).

$\begin{figure} \centerline {\hbox{ \psfig{file=sketch1.ps,width=4.5cm} \psfig{file=sketch2.ps,width=4.5cm} \psfig{file=sketch3.ps,width=4.5cm}}}\end{figure}$

**Figure:** Schematic sketch to illustrate the problem of *self-shadowing* (symbols are explained in the text).
$\begin{figure} \centerline {\hbox{ \psfig{file=sketch1.ps,width=4.5cm} \psfig{file=sketch2.ps,width=4.5cm} \psfig{file=sketch3.ps,width=4.5cm}}}\end{figure}$

In a next step, line blocking was treated consistently. Using the method of the non-LTE Hopf functions this is an easy task, since we just have to update the parameters involved by a flux-correction procedure applied at different values of the optical-depth scale (cf. Pauldrach et al. 1997). As can be inferred from Fig. 6 the flux is conserved again for this model with an accuracy of a few per cent.

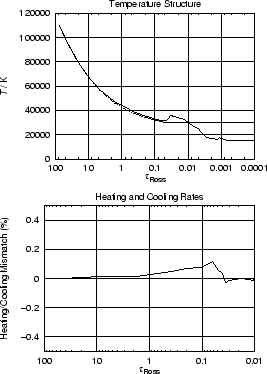
Figure 7 displays the resulting temperature structure and shows that the temperature increases by 2000K at $\tau_{\rm Ross}^{}$ = 1. Also shown is the mismatch of the heating and cooling rates, which immediately goes to zero in the outer part ( $\tau_{\rm Ross}^{}$ < 0.07) where it is applied for correcting the temperature structure. This produces the pronounced hump and the successive decrease of the temperature in this part.

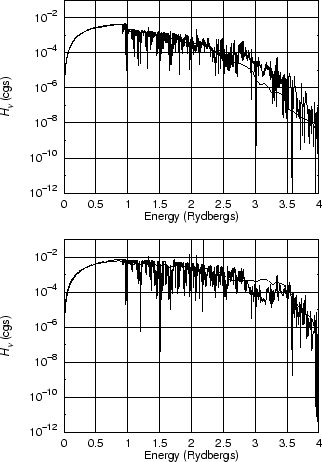
In Fig. 8 we compare our calculated EUV blocking spectrum with the emergent fluxes from an appropriate Kurucz (1992) model which is based on LTE and plane-parallel static atmospheres. An important point shown is that we obtain almost the same blanketing effect as Kurucz. This is inferred from the redward side of the H edge where the curves are nearly identical, and thus the temperature has to rise in the continuum-forming region in the same way for both models. As absorptive opacities necessarily dominate in LTE, this result requires the same for our model at least for optical depths larger than 0.1. We have already mentioned this finding above. Another important feature observed in Fig. 8 is that the line blocking is less pronounced for our model above 2.7 Ryd; hence we obtain more flux in this frequency range. The opposite result, however, was found for a supergiant model with an effective temperature of T_eff = 50 000 K (henceforth O50). As is shown in Fig. 8 (lower panel), less flux appears for our model above 2.7 Ryd, and the blanketing effect is also slightly less pronounced. We attribute the latter result to the influence of the strong wind (mass-loss rate of $\dot{M}$ = 12 x 10^-6 M $\scriptstyle \odot$ /yr) on the density structure, which is very different from the static case.

The most surprising result observed so far for our O50 model is the strong absorption features which originate in the outer, and hence scattering, part of the wind. As these features are not balanced by corresponding emission features (in a pure scattering atmosphere this has to be the case in order to conserve the energy), and as this hot star emits most of its flux in the EUV blocking part, we should observe a considerable flux deviation.

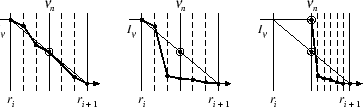
Figure 9 (upper panel) shows that this is indeed the case - flux is not conserved by up to 20% in the scattering-dominated part of the wind. This is the result of an inconsistency which became evident for the O50 model, because of the strong wind which favours the influence of scattering lines on the emergent EUV spectrum in the outer part of the atmosphere. The reason for this inconsistency is self-shadowing - i.e.,the interaction of strong wind lines with themselves. It occurs because the incident intensity used to calculate the bound-bound transition rates for any arbitrary line is already affected by that particular line itself, since the line has already been treated for line blocking in the iteration cycle. We refer to the schematic sketch above to illustrate this point.

In a given velocity interval, between successive radial depths points, r_i $\rightarrow$ r_{i + 1}, we need to estimate the intensity I $\scriptstyle \nu$ (indicated by dots) seen by lines (indicated by dashes) contained in the equivalent frequency interval. In general, we use the intensity I $\scriptstyle \nu_{n}$ (indicated by $\odot$ ) calculated at the sampling point (indicated by $\nu_{n}^{}$ ), which represents a fair mean value for the true incident radiation of the individual lines in this interval, provided all the lines are of similar strength (see left panel of Fig. 10).

However, if there is a dominating line in the interval (middle panel of Fig. 10), the intensity taken at the sampling point (and used for the bound-bound transitions belonging to lines in this interval) is much smaller than the true incident radiation for this line, because the line has already influenced this value considerably. This is what we mean by self-shadowing. The consequences are that the source function of this line is underestimated; thus, the scattering processes are not correctly described, and, hence, energy is not conserved. The solution, however, is quite simple. For calculating the bound-bound rates - having identified the dominating lines - we just irradiate them by an incident intensity which is independent of the lines in the considered interval (right panel of Fig. 10). With this correction the flux is conserved again as shown in Fig. 9 (lower panel).

Figure: Comparison of EUV spectra from our O50 supergiant model ( T_eff = 50 000 K, log g = 3.8) with (fully drawn) and without (dotted) corrections for self-shadowing.

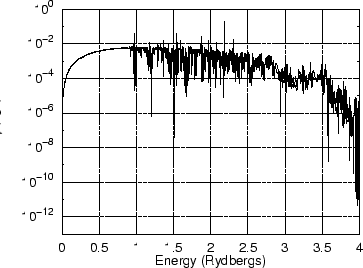$\begin{figure} \centerline {\hbox{ \psfig{file=22-s50.ps,angle=-90,width=14cm}}}\end{figure}$

**Figure:** Comparison of EUV spectra from our O50 supergiant model ( T_eff = 50 000 K, log g = 3.8) with (fully drawn) and without (dotted) corrections for self-shadowing.
$\begin{figure} \centerline {\hbox{ \psfig{file=22-s50.ps,angle=-90,width=14cm}}}\end{figure}$

A comparison of the EUV blocking spectra calculated with and without this correction procedure (see Fig. 11) shows that the strong absorption features vanished, and the smaller ones are now compensated by corresponding emission features.